Question

A plane rises from take-off and flies at an angle of 7° with the horizontal runway. When it has gained 800 feet, find the distance, to the nearest foot, the plane has flown.

Answer 1

To solve this problem, we can use trigonometry. Let x be the distance flown by the plane. Then, we can use the tangent function to find x:

`\qquad\quad\dashrightarrow\:\:\tan(7^\circ) = (800)/(x)`

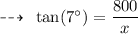
Multiplying both sides by x, we get:

`\qquad\qquad\dashrightarrow\:\: x \tan(7^(\circ)) = 800`

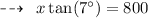
Dividing both sides by
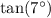`\tan(7^(\circ))`, we get:

`\qquad\qquad\dashrightarrow\:\: x = (800)/(\tan(7^(\circ)))`

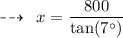
Using a calculator, we find that:

`\qquad\qquad\dashrightarrow\:\:\tan(7^(\circ)) \approx 0.122`

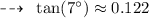
We have:

`\qquad\dashrightarrow\:\: x \approx (800)/(0.122) \approx \bold{6557.38}`

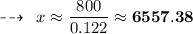
`\therefore`To the nearest foot, the distance flown by the plane is 6557 feet.

`\blue{\overline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}}`