The exact value of the arc length of the curve is 123.81 units
How to determine the exact arc length of the curve
From the question, we have the following parameters that can be used in our computation:
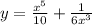
Also, we have the interval to be
x = 2 to x = 5
The arc length of the curve can be calculated using

Recall that
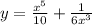
So, we have
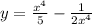
So, we have
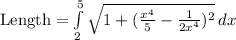
This gives
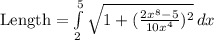
Expand

Next, we have
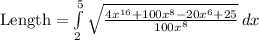
Using a graphing tool, we have the integrand to be
Length = 123.81
Hence, the exact arc length of the curve is 123.81 units