Question

Find the LCD and build up each rational expression so they have a common denominator. (5)/(m^(2)-5m+4),(6m)/(m^(2)+8m-9)

Answer 1

`(5m+45)/(m^3+4m^2-41m+36),\quad(6m^2-24m)/(m^3+4m^2-41m+36)`

Explanation:

You want the rational expressions written with a common denominator:

(5)/(m^(2)-5m+4), (6m)/(m^(2)+8m-9)

Factors

Each expression can be factored as follows:

`(5)/(m^2-5m+4)=(5)/((m-1)(m-4)),\quad(6m)/(m^2+8m-9)=(6m)/((m-1)(m+9))`

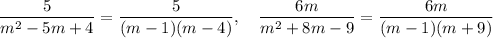
Common denominator

The factors of the LCD will be (m -1)(m -4)(m +9). The first expression needs to be multiplied by (m+9)/(m+9), and the second by (m-4)/(m-4).

Expressed with a common denominator, the rational expressions are ...

`(5(m+9))/((m-1)(m-4)(m+9)),\quad(6m(m-4))/((m-1)(m-4)(m+9))`

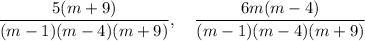
In expanded form, the rational expressions are ...

`\boxed{(5m+45)/(m^3+4m^2-41m+36),\quad(6m^2-24m)/(m^3+4m^2-41m+36)}`

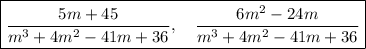
<95141404393>