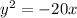Question

find the equationof he parabola, with vertex at origin, axis of symmetry at x-axis and directrixat x=5

Answer 1

Explanation:

The equation of parabola if we are interested in the directrix either

`(x - h) {}^(2) = 4p(y - k)`

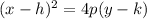
or

`(y - k) {}^(2) = 4p(x - h)`

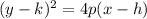
Since this parabola is symmetric about the x axis, and we have a vertical directrix, we will use the second parabola equation

`(y - k) {}^(2) = 4p(x - h)`

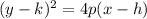
Here (h,k) is the vertex, so h and k are 0

`{y}^(2) = 4px`

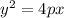
What is the value of P.

The value of P is the displacement of the vertex to either the focus or directrix.

Since the directrix is right of the vertex, our p will be negative.

The distance between the vertex and directrix is -5.

Long story short: the shortest displacement between a line and a point is the perpendicular dispalcement , which would be -5.

`{y}^(2) = 4( - 5)x`

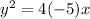
Our answer is

`{y}^(2) = - 20x`