Question

Here is Takeshi's work determining a third point on the graph of an exponential function, `h(x)`.

Explain why the work is incorrect.

Answer 1

Explanation:

Let h(x) = y

The exponentail function is of the form :

`y = ab^x`

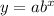
We have :

`y_(_1) = ab^{x_(_1)}\\y_(_2) = ab^{x_(_2)}\\\\\implies (y_(_1))/(y_(_2)) = \frac{ab^{x_(1)}}{ab^{x_(2)}} \\\\\implies (y_(_1))/(y_(_2)) = \frac{b^{x_(1)}}{b^{x_(2)}} \\\\\implies (y_(_1))/(y_(_2)) = b^((x_1-x_2))`

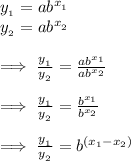
Given points : (4, 9) and (5, 34.2)

We have:

`(34.2)/(9) = b^((5-4))\\\\\implies 3.8 = b`

Writing the equation with x, y and b:

`y = ab^x\\\\\implies 9 = a(3.8^4)\\\\a = (9)/(3.8^4) \\\\a = 0.043`

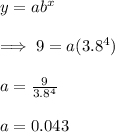
a = 0.043

b = 3.8

When x = 6, y will be:

`y = (0.043)(3.8^6)\\\\y = 128.47`

This is not the y value in the question y = 59.4

Therefore (6, 59.4) does not lie on the graph h(x)