Question

Write the equation of the line that has a rate of change of 5 and passes through the point

(4, -1)

Answer 1

The point-slope form of a linear equation is y - y1 = m(x - x1), where m is the slope and (x1, y1) is a point on the line.

We are given that the rate of change (slope) is 5 and that the line passes through the point (4, -1).

Substituting the values into the point-slope form, we get:

y - (-1) = 5(x - 4)

Simplifying the equation, we get:

y + 1 = 5x - 20

y = 5x - 21

Therefore, the equation of the line that has a rate of change of 5 and passes through the point (4, -1) is y = 5x - 21.

Answer 2

Hello

Answer:

`\Large \boxed{\sf y=5x-21}`

Explanation:

The slope-intercept form of a line equation is
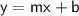`\sf y=mx+b` where m is the rate of change (or the slope) and b is the y-intercept.

We know that the rate of change is 5 so :
`\boxed{\sf m=5}`

`\sf y=5x+b`

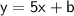
Let's find the value of b !

Moreover, we know that the line passes through the point (4,-1).

Let's replace x and y with 4 and -1 in the equation and solve for b:

`\sf -1=4*5+b`

`\sf\iff -1=20+b`

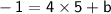
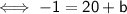
Let's substract 20 from both sides :

`\sf -1-20=20-20+b`

`\boxed {\sf b=-21}`

The equation of the line is :
`\boxed{\sf y=5x-21}`

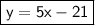
Have a nice day ;)