Question

Calculus i need help !
Calculate the integral

Answer 1

`5.80013+3.29613i`

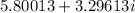
Explanation:

Calculate the given double integral.

`\int\limits^4_0 {\int\limits^(√(4y-y^2) )_0 {√(8-x^2-y^2) } \, dx } \, dy`

`\hrulefill`

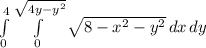
After attempting to solve this integral by hand, I found out quickly that this integral is way too complex to solve. I had to resort to a computing software to get an approximated solution. Here is what I got,

`\int\limits^4_0 {\int\limits^(√(4y-y^2) )_0 {√(8-x^2-y^2) } \, dx } \, dy=\boxed{\boxed{5.80013+3.29613i}}`

Below is all the work I had done before I stopped. I left my work here in case you wanted to take a peek. Other than that you can ignore it, as it ended up not being very useful.
`\hrulefill`

(1) - Rearranging the integrand

`\int\limits^4_0 {\int\limits^(√(4y-y^2) )_0 {√(8-x^2-y^2) } \, dx } \, dy\\\\\\\Longrightarrow \int\limits^4_0 {\int\limits^(√(4y-y^2) )_0 {√(8-y^2-x^2) } \, dx } \, dy`

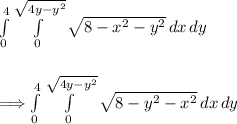
(2) - Applying trigonometric substitution to evaluate the first integral

`\boxed{\left\begin{array}{ccc}\text{For} \ √(a-bx^2) \\\\ \rightarrow x=\sqrt{(a)/(b) }\sin(u) \end{array}\right}`

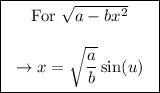
Note that every term not containing an "x" is held constant. Thus, we can say:

`a=8-y^2\\\\b=1\\\\\sqrt{(a)/(b) }=\sqrt{(8-y^2)/(1) } =√(8-y^2) \\\\\\\therefore \boxed{x=√(8-y^2) \sin(u) \ \text{and} \ dx=√(8-y^2) \cos(u)du}`

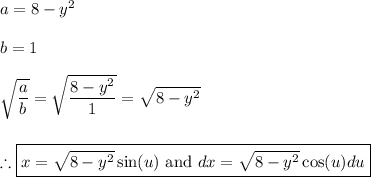
Substituting in the values:

`\int\limits^4_0 {\int\limits^(√(4y-y^2) )_0 {√(8-y^2-x^2) } \, dx } \, dy\\\\\\\Longrightarrow \int\limits^4_0 {\int\limits^(√(4y-y^2) )_0 {\sqrt{8-y^2-(√(8-y^2) \sin(u))^2} \cdot √(8-y^2) \cos(u) } \, du } \, dy`

Simplifying the integrand:

`\int\limits^4_0 {\int\limits^(√(4y-y^2) )_0 {\sqrt{8-y^2-(√(8-y^2) \sin(u))^2} \cdot √(8-y^2) \cos(u) } \, du } \, dy\\\\\\\\\Longrightarrow \int\limits^4_0 {\int\limits^(√(4y-y^2) )_0 {√(8-y^2-\sin^2(u)(8-y^2)) \cdot √(8-y^2) \cos(u) } \, du } \, dy\\\\\\\\\Longrightarrow \int\limits^4_0 {\int\limits^(√(4y-y^2) )_0 {√(8-y^2-8\sin^2(u)+y^2\sin^2(u)) \cdot √(8-y^2) \cos(u) } \, du } \, dy`

`\Longrightarrow \int\limits^4_0 {\int\limits^(√(4y-y^2) )_0 {√((1-\sin^2(u))(8-y^2))} \cdot √(8-y^2) \cos(u) } \, du } \, dy`

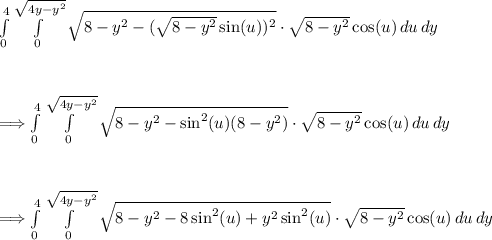
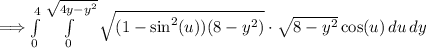
Applying the Pythagorean identify:

`\boxed{\left\begin{array}{ccc}\text{\underline{Pythagorean Identity:}}\\\\1-\sin^2{A}=\cos^2(A)\end{array}\right}`

`\Longrightarrow \int\limits^4_0 {\int\limits^(√(4y-y^2) )_0 {√(\cos^2(u)(8-y^2))} \cdot √(8-y^2) \cos(u) } \, du } \, dy`

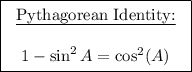
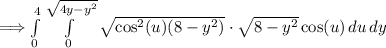
Applying the following radical rule:

`√(ab)=√(a)√(b)`

`\Longrightarrow \int\limits^4_0 {\int\limits^(√(4y-y^2) )_0 {√(\cos^2(u))√(8-y^2)} \cdot √(8-y^2) \cos(u) } \, du } \, dy\\\\\\\\\Longrightarrow \int\limits^4_0 {\int\limits^(√(4y-y^2) )_0 {\cos(u)√(8-y^2)} \cdot √(8-y^2) \cos(u) } \, du } \, dy\\\\\\\\\Longrightarrow \boxed{ \int\limits^4_0 {\int\limits^(√(4y-y^2) )_0 {\cos^2(u)(8-y^2) } \, du } \, dy}`

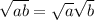
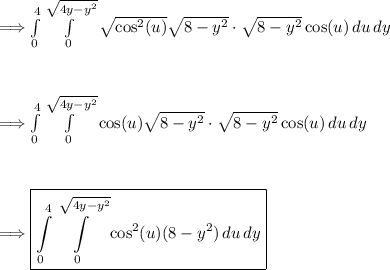
(3) - Adjusting the integral boundaries

`\text{Recall,} \ x=√(8-y^2) \sin(u)`

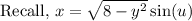
Solve for "u"

`x=√(8-y^2)\sin(u) \\\\\\\Longrightarrow \sin(u)=(x)/(√(8-y^2)) \\\\\therefore \boxed{u=\sin^(-1)\Big((x)/(√(8-y^2))\Big)}`

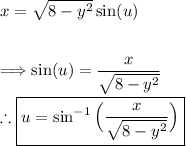
Adjusting the upper bound:

`x_(upper)=√(4y-y^2)\\ \\\\\Longrightarrow u_(upper)=\sin^(-1)\Big((√(4y-y^2))/(√(8-y^2))\Big)`

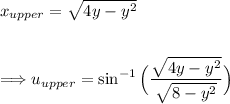
Adjusting the lower bound:

`x_(lower)=0\\ \\\\\Longrightarrow u_(lower)=\sin^(-1)\Big((0)/(√(8-y^2))\Big)\\\\\\\Longrightarrow u_(lower)=\sin^(-1)(0)\\\\\\\Longrightarrow u_(lower)=0`

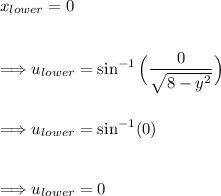
Now we have the following integral,

`\int\limits^4_0 {\int\limits^{\sin^(-1)((√(4y-y^2) )/(√(8-y^2) ))}_0 {\cos^2(u)(8-y^2) } \, du } \, dy`

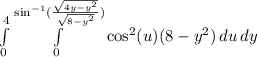
(4) - Evaluating the first integral

`\int\limits^4_0 {\int\limits^{\sin^(-1)((√(4y-y^2) )/(√(8-y^2) ))}_0 {\cos^2(u)(8-y^2) } \, du } \, dy`

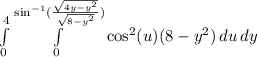
Pulling out the constant:

`\Longrightarrow \int\limits^4_0 \Big[(8-y^2)\int\limits^{\sin^(-1)((√(4y-y^2) )/(√(8-y^2)))}_0 {\cos^2(u)} \, du\Big]dy`

Applying the square-to-linear identity:

`\boxed{\left\begin{array}{ccc}\text{\underline{Square-to-Linear Identity:}}\\\\\cos^2(A)=(1)/(2)+(1)/(2)\cos(2A) \end{array}\right}`

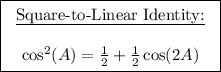
`\Longrightarrow \int\limits^4_0 \Big[(8-y^2)\int\limits^{\sin^(-1)((√(4y-y^2) )/(√(8-y^2)))}_0 {(1)/(2)+(1)/(2)\cos(2u) } \, du\Big]dy\\\\\\\\\Longrightarrow \int\limits^4_0 {(8-y^2)\Big[(1)/(2)u+(1)/(4)\sin(2u) \Big]\limits^{\sin^(-1)((√(4y-y^2) )/(√(8-y^2)))}_0} \, dy \\\\\\\\`

`\Longrightarrow \int\limits^4_0 {(8-y^2)\Big[(1)/(2)(\sin^(-1)((√(4y-y^2) )/(√(8-y^2))))+(1)/(4)\sin(2\sin^(-1)((√(4y-y^2))/(√(8-y^2) ) )\Big]\, dy \\`

This is where I stopped^^