Question

F maps (0,1)→(0,1). Fix)ulo if x is ierational and 1/q if x is rational with reduced form p/q, for p \& a relatively prime integeth. Which of the following is correct: Pick ONE option Fis continuous on its full domain Fis nowhere continuous Fis continuous on the irrationals but not on the rationals Fis continuous on the rationals but not on the irrationals

Answer 1

The function F maps the interval (0,1) to the interval (0,1) and is defined differently for rational and irrational numbers. F is continuous on the irrationals but discontinuous on the rationals.

Step-by-step explanation:

The function F maps the interval (0,1) to the interval (0,1) and is defined as follows:

1. If x is an irrational number, then F(x) = the fractional part of x.
2. If x is a rational number in lowest terms p/q, then F(x) = 1/q.

In other words, F(x) gives the fractional part of an irrational number and the reciprocal of the denominator for a rational number in lowest terms.

To determine the continuity of the function F, we need to consider its behavior on the rational and irrational numbers separately:

change

1. F is continuous on the irrational numbers since the fractional part of any irrational number is always continuous.
2. F is discontinuous on the rational numbers. This is because the value of F jumps discontinuously from one rational number to another when the denominator changes.

Therefore, the correct statement is: F is continuous on the irrationals but not on the rationals.

Answer 2

F is continuous on the irrationals but not on the rationals.

Step-by-step explanation:

The function F defined as
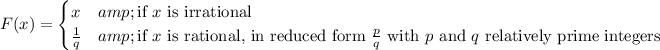`\( F(x) = \begin{cases} x & \text{if } x \text{ is irrational} \\ (1)/(q) & \text{if } x \text{ is rational, in reduced form } (p)/(q) \text{ with } p \text{ and } q \text{ relatively prime integers} \end{cases} \)` exhibits continuity on the irrationals and discontinuity on the rationals.

For irrational numbers in the interval (0, 1), the function behaves as the identity function,
`\( F(x) = x \)`, which is continuous. However, for rational numbers in the same interval, the function becomes
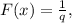`\( F(x) = (1)/(q) \),` introducing a jump discontinuity at each rational point. This leads to F being continuous on the irrationals but not on the rationals.

The reason for this behavior lies in the fact that the rational numbers are dense in the real number line, creating a situation where the function jumps between two values at every rational point. The irrationals, on the other hand, do not exhibit such jumps, allowing for continuous behavior on that subset of the domain.