Question

Brian creates the graph of function g by applying a transformation to function f:

f(x)=4^x+1
g(x)=1/8(4)^x+1
Which transformation did Brian apply?


a vertical compression by a factor of 1/8

a vertical stretch by a factor of 8

a horizontal stretch by a factor of 8

a horizontal compression by a factor of 1/8

Please help worth 20 pts.

Answer 1

a vertical compression by a factor of
`(1)/(8)`

Explanation:

Start with the original function
`f(x) = 4^x+1`.

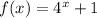Apply the vertical compression by multiplying the function by
`(1)/(8)`:

`g(x) = ((1)/(8) ) * 4^x+1`.

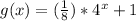Simplify the expression:

`g(x) = (1)/(8) * 4^x * 4^1`.

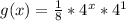Use the property of exponents
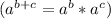`(a^(b+c) = a^b * a^c)` to simplify further:

`g(x) = (1)/(8) * (4^x * 4)`.

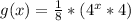Simplify the expression inside the parentheses:

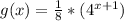`g(x) = (1)/(8) * (4^(x+1) )`.

Answer 2

a vertical compression by a factor of 1/8

Explanation: