Question

Heeeeeeeeeellllllllllppppppppppppp

Answer 1

`\overline{AB}=28`

`\overline{BC}=17.5`

`x=13.2`

Explanation:

Question 4

If quadrilateral PQRS is similar to quadrilateral ABCD, their corresponding sides are in the same ratio:

`\overline{PQ} : \overline{AB} = \overline{QR} : \overline{BC} = \overline{RS} : \overline{CD} = \overline{SP}:\overline{DA}`

From inspection of the two quadrilaterals, the given side lengths are:

`\overline{PQ} = 8`

`\overline{QR} = 5`

`\overline{RS} = 6`

`\overline{SP} = 4`

`\overline{DA} = 14`

Substitute these into the ratio equation:

`8 : \overline{AB} = 5 : \overline{BC} = 6 : \overline{CD} = 4:14`

Solve for AB:

`8 : \overline{AB} = 4:14`

`\frac{8}{\overline{AB}}= (4)/(14)`

`8 \cdot 14=4 \cdot{\overline{AB}}`

`\overline{AB}=(8 \cdot 14)/(4)`

`\boxed{\overline{AB}=28}`

Solve for BC:

`5 : \overline{BC} = 4:14`

`5 \cdot 14=4 \cdot \overline{BC}`

`\overline{BC}=(5 \cdot 14)/(4)`

`\boxed{\overline{BC}=17.5}`

`\hrulefill`

Question 5

Assuming the two figures are similar, their corresponding sides are in the same ratio. Therefore:

`x:6=11:5`

`(x)/(6)=(11)/(5)`

`x=(11 \cdot 6)/(5)`

`x=(66)/(5)`

`\boxed{x=13.2}`

Answer 2

AB = 28 , BC = 17.5 , X = 13.2

Explanation:

since the figures are similar then the ratios of corresponding sides are in proportion, that is

`(AB)/(PQ)` =
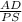`(AD)/(PS)` ( substitute values )

`(AB)/(8)` =
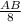`(14)/(4)` ( cross- multiply )

4 AB = 8 × 14 = 112 ( divide both sides by 4 )

AB = 28

and

`(BC)/(QR)` =
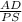`(AD)/(PS)` ( substitute values )

`(BC)/(5)` =
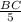`(14)/(4)` ( cross- multiply )

4 BC = 5 × 14 = 70 ( divide both sides by 4 )

BC = 17.5

similarly for the 2 similar figures

`(x)/(6)` =
`(11)/(5)` ( cross- multiply )

5x = 6 × 11 = 66 ( divide both sides by 5 )

x = 13.2