Question

What is the explicit formula for this sequence?

-16, -19, -22, -25,...
A. an= (-3) + (n − 1)(-16)
OB. an= (-28) + (n − 1)(-3)
OC. an= (-16) + (n − 1)3
OD. an= (-16)+(n-1)(-3)
SUBMIT

Answer 1

D. aₙ = (-16) + (n - 1)(-3)

Explanation:

An explicit formula for a sequence allows you to find the nth term of the sequence.

The given sequence is arithmetic as it has a common difference of -3 between terms. Each term is 3 less than the previous term:

`a_1=-16`

`a_2=a_1-3=-16 - 3 = -19`

`a_3=a_2-3=-19 - 3 = -22`

`a_4=a_3-3=-22 - 3 = -25`

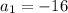
The general formula to find the nth term (aₙ) of an arithmetic sequence is:

`\boxed{\begin{minipage}{8 cm}\underline{General form of an arithmetic sequence}\\\\$a_n=a+(n-1)d$\\\\where:\\\phantom{ww}$\bullet$ $a_n$ is the nth term. \\ \phantom{ww}$\bullet$ $a$ is the first term.\\\phantom{ww}$\bullet$ $d$ is the common difference between terms.\\\phantom{ww}$\bullet$ $n$ is the position of the term.\\\end{minipage}}`

Substitute a = -16 and d = -3 into the formula:

`a_n=(-16)+(n-1)(-3)`

Therefore, the matching answer option is option D.

Answer 2

D

Explanation:

the sequence has a common difference between consecutive terms, that is

- 19 - (- 16) = - 19 + 16 = - 3

- 22 - (- 19) = - 22 + 19 = - 3

- 25 - (- 22) = - 25 + 22 = - 3

this indicates the sequence is arithmetic with explicit formula

`a_(n)` = a₁ + (n - 1)d

here a₁ = - 16 and d = - 3 , then

`a_(n)` = - 16 + (n - 1)(- 3)