Question

Given that the pattern for the data concerning the heights for students attending a secondary institution is bell-shaped, approximate the percentage of the distribution with values lying between 114 cm and 132 cm if the mean and standard deviation for the distribution are equal to 150 cm and 18 cm respectively

Answer 1

The percentage of the distribution with values lying between 114 cm and 132 cm is 13.59%

Explanation:

Mean = M = 150 cm

Standard Deviation = S = 18 cm

Now, since the pattern is bell shaped, we can use the normal distribution to find the probabilities using z-values.

To find the probability that height lies between 114 cm and 132 cm, we find the probability that height is lower than 114 cm and same for 132 cm and then subtract the two to get the probability for having height in between these two.

Height lower than 114 cm

P(X<114)

Finding z value, using,

`z = (x - M)/S\\z = (114 - 150)/18\\z = -36/18\\z=-2`

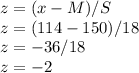
This corresponds to the probability, (looking up the value in a z-table)

P(X<114) = 0.0228

Height lower than 132 cm,

P(X<132)

Finding z value,

`z =(x-M)/S\\z = (132-150)/18\\z = -18/18\\z=-1`

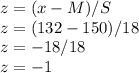
Looking up the corresponding probability value from a table,

we get, for z = -1,

P(X < 132) = 0.1587

Then, finally,

Height in between 114 and 132,

P(114 < X < 132)

P(114 < X < 132) = P(X<132) - P(X<114)

= 0.1587 - 0.0228

P(114 < X < 132) = 0.1359

or,

P(114 < X < 132) = 13.59%