Question

Find the equation of the line through (−7,6) that is parallel to the line y=−2x+6.

Answer 1

The answer is:

y = -2x - 8

Step-by-step explanation:

Parallel lines have equal slopes; knowing that the slope of y = -2x + 6 is -2, we also know that the slope of the line that is parallel to y = -2x + 6 is -2.

Now, let's plug the data into point slope.

Point slope is
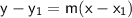`\sf{y-y_1=m(x-x_1)}`, where m is the slope and (x₁, y₁) is a point on the line.

`\sf{y-6=-2(x-(-7)}`

Simplify.

`\sf{y-6=-2(x+7)}`

`\sf{y=-2x-14+6}`

`\sf{y=-2x-8}`

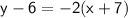
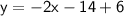
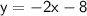
Hence, the equation is y = -2x - 8.

Answer 2

Answer: y = -2x - 8

Step-by-step explanation:

The given line has slope m = -2

Parallel lines have an equal slope, but their y intercepts are different.

Use point slope form to get the following.

y - y1 = m(x - x1)

y - 6 = -2(x - (-7))

y - 6 = -2(x + 7)

y - 6 = -2x - 14

y = -2x - 14 + 6

y = -2x - 8