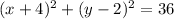Question

Identify the center and radius of the circle from the below plot then write the standard form equation.

The center of the circle is ( , ).
The radius of the circle is
The standard form equation of the circle is

Answer 1

The center of the circle is (-4, 2).

The radius of the circle is 6 units.

The standard form equation of the circle is
`(x+4)^2+(y-2)^2=36`

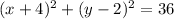
Explanation:

To find the center of the circle, you must find the middle, or the center point of the circle. That will be at (-4, 2).

The radius is a straight line extending from the center of a circle

To find the radius of the circle, start with the center of the circle, (-4, 2), and extend in a straight line (doesn't matter if you go up, down, left or right) and count how much units. You get that the radius of the circle is 6 units.

The standard equation of a circle is:

`(x-h)^2+(y-k)^2=r^2`

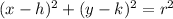
Where h and k is your x and y coordinates from the center point, and r is your radius.

The standard form equation of this circle would be:

`(x+4)^2+(y-2)^2=36`

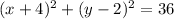
You may be wondering why the 4 is positive and why there is a 36 at the end.

The 4 is positive because when plugging the coordinates of the center point (-4, 2) into the equation of a circle, you first place every thing as:

(x - (-4))^2 + (y - (2))^2 = (6)^2

The negatives sign cancel each other out and turn into a positive sign. Also the radius, 6, is squared, meaning multiplied to its self, so that's why there is a 36 at the end.

`(x+4)^2+(y-2)^2=36`