Question

This graph relates the area of a face of a cube to the surface area of that cube. Surface Area of Cubes On a coordinate plane, the x-axis is labeled Area of a Face of a Cube and the y-axis is labeled Surface Area of a Cube. A line goes through points (0, 0), (1, 6), and (2, 12). Which ordered pair is also on the line relating the area of a face of a cube and the surface area of the cube?

Answer 1

The line described in the graph is a straight line passing through the origin (0,0) and has a constant slope. The slope of the line can be calculated using any two points on the line. Here, we can use the points (0,0) and (1,6). The slope (m) is given by the formula:

`$$m = (y_2 - y_1)/(x_2 - x_1)$$`

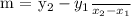
Substituting the coordinates of the two points into the formula, we get:

`$$m = (6 - 0)/(1 - 0) = 6$$`

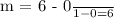
So, the slope of the line is 6. This means that for every unit increase in the x-coordinate (Area of a Face of a Cube), the y-coordinate (Surface Area of a Cube) increases by 6 units.

Therefore, if we want to find an ordered pair that is also on the line, we can choose an x-coordinate and multiply it by the slope to get the corresponding y-coordinate. For example, if we choose an x-coordinate of 3, the y-coordinate would be 3 * 6 = 18. So, the ordered pair (3, 18) is also on the line relating the area of a face of a cube and the surface area of the cube.