Question

For the following exercise, solve the equation by identifying the quadratic form. Use a substitute variable and find all real solutions by factoring. (x+2)^(2)-25=0

Answer 1

Explanation:

This is a quadratic equation in the form of

vertex form

`(x - h) {}^(2) + k`

where (-2,-25) is the vertex in this case.

`(x + 2) {}^(2) - 25 = 0`

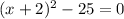
Let u equal x+2

`{u}^(2) - 25 = 0`

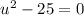
Use difference of squares and we get

`(u - 5)(u + 5) = 0`

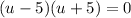
For the first binomial

`u - 5 = 0`

`u = 5`

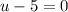
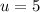
Remember u=x+2

`x + 2 = 5`

`x = 3`

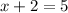
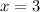
For the Second Binomial, repeat the steps above

`x + 2 = - 5`

`x = - 7`

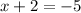
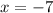
So our solutions are 3 and -7