Question

Identify the common difference and write an equation for the given arithmetic sequence. Ther find the 45th term. 36,30,24,18,........

Answer 1

45th term = -228

Explanation:

The formula to find the nth term of an arithmetic sequence is:

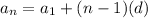`a_(n)=a_(1)+(n-1)(d)`, where

• a1 is the first term,
• n is the term position (e.g., 1st or 46th),
• and d is the common difference.

Step 1: Identify a1, the firs term:

The first term is 36.

Step 2: Find d, the common difference:

• We can find d, the common difference, by subtracting two consecutive terms with the preceding term being subtracted from a succeeding term.

We can subtract 36 from 30:

d = 30 - 36

d = -6

Thus, the common difference is d.

Step 2: Plug in 36 for a1, 45 for n, and -6 for d to find a(45), the 45th term:

`a_(45)=36+(45-1)(-6)\\ a_(45)=36+(44)(-6)\\ a_(45)=36-264\\ a_(45)=-228`

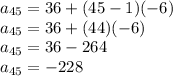
Thus, the 45th term is -228.