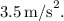Question

A block is pushed up a frictionless 30

∘
incline by an applied force as shown. If F=25 N and M=3.0 kg, what is the magnitude of the resulting acceleration of the block? 4.6 m/s
∧
2 2.9 m/s
∧
2 3.5 m/s
∧
2 2.3 m/s
∧
5 5.1 m/s
∧
2

Answer 1

The magnitude of the resulting acceleration of the block is approximately
`\( 3.43 \, \text{m/s}^2 \)`,

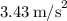Let's solve the problem step by step:

Step 1: Break down the forces acting on the block

On a frictionless incline, there are two main forces acting on the block:

1. The gravitational force acting downwards (the weight of the block,
`\( w = m \cdot g \)).`

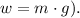
2. The applied force pushing the block up the incline (given as
`\( F = 25 \, \text{N} \)).`

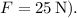
Step 2: Calculate the component of gravitational force acting along the incline

The component of the gravitational force acting down the incline can be calculated using the angle
`\( F = 25 \, \text{N} \)).`

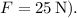
Step 3: Calculate the net force along the incline

The net force along the incline is the applied force minus the gravitational force component along the incline:

`\[ F_{\text{net}} = F - m \cdot g \cdot \sin(\theta) \]`

Step 4: Use Newton's second law to find the acceleration

Newton's second law states that
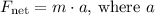`\( F_{\text{net}} = m \cdot a \), where \( a \)` is the acceleration. To find the acceleration, rearrange this to:

`\[ a = \frac{F_{\text{net}}}{m} \]`

Step 5: Calculate the acceleration

Given values:

-
`\( m = 3.0 \, \text{kg} \)`

-
`\( g = 9.8 \, \text{m/s}^2 \)`

-
`\( \theta = 30^\circ \)`

-
`\( F = 25 \, \text{N} \)`

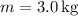
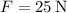
Calculate the gravitational force component:

`\[ m \cdot g \cdot \sin(\theta) = 3.0 \, \text{kg} * 9.8 \, \text{m/s}^2 * \sin(30^\circ) \]`

Calculate the net force:

`\[ F_{\text{net}} = F - m \cdot g \cdot \sin(\theta) \]`

Calculate the acceleration:

`\[ a = \frac{F_{\text{net}}}{m} \]`

Let's perform these calculations.

Following the stepwise solution:

Step 2: The gravitational force component along the incline is:

`\[ 3.0 \, \text{kg} * 9.8 \, \text{m/s}^2 * \sin(30^\circ) = 14.7 \, \text{N} \]`

Step 3: The net force acting along the incline is:

`\[ 25 \, \text{N} - 14.7 \, \text{N} = 10.3 \, \text{N} \]`

Step 4 & 5: The resulting acceleration of the block is:

`\[ \frac{10.3 \, \text{N}}{3.0 \, \text{kg}} = 3.43 \, \text{m/s}^2 \]`

The magnitude of the resulting acceleration of the block is approximately
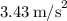`\( 3.43 \, \text{m/s}^2 \)`, which is closest to the provided option of
`\( 3.5 \, \text{m/s}^2 \).`

Answer 2

The magnitude of the resulting acceleration of the block is determined as 3.43 m/s².

How to calculate the magnitude of the resulting acceleration of the block?

The magnitude of the resulting acceleration of the block is calculated by applying Newton' second law of motion as follows;

F(net) = ma

F - mg sinθ = ma

where;

• m is the mass of the block
• g is acceleration due to gravity
• a is the acceleration of the block
• F is the applied force

a = (F - mg sinθ) / m

a = (25 - 3 x 9.8 x sin30) / 3

a = 3.43 m/s²

Thus, the magnitude of the resulting acceleration of the block is determined as 3.43 m/s².