Question

Children playing in a playground on the flat roof of a city school lose their ball to the parking lot below. One of the teachers kicks the ball back up to the children as shown in the figure below. The playground i 6.30 m above the parking lot, and the school building's vertical wall is h = 7.40 m high, forming a 1.10 m high railing around the playground. The ball is launched at an angle of 0 = 53.0° above the horizontal

a point d = 24.0 m from the base of the building wall. The ball takes 2.20s to reach a point vertically above the wall. (Due to the nature of this problem, do not use rounded intermediate values in your

calculations-including answers submitted in WebAssign.)


(a) Find the speed (in m/s) at which the ball was launched.

m/s

(b) Find the vertical distance (in m) by which the ball clears the wall.

(c) Find the horizontal distance (in m) from the wall to the point on the roof where the ball lands.

E

(d) What If? If the teacher always launches the ball with the speed found in part (a), what is the minimum angle (in degrees above the horizontal) at which he can launch th

railing? (Hint: You may need to use the trigonometric identity sec?(0) = 1 + tan (0).)

° above the horizontal

13

(e)

What would be the horizontal distance (in m) from the wall to the point on the roof where the ball lands in this case?

m

ball and still clear the playground

755 PM

26/09/2022

Answer 1

(a) The speed at which the ball was launched is approximately
`\( 18.14 \ \text{m/s} \)`.

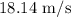(b) The vertical distance by which the ball clears the wall is approximately
`\( 14.50 \ \text{m} \)`.

(c) The horizontal distance from the wall to the point on the roof where the ball lands is
`\( 24.0 \ \text{m} \)`.

(d) The minimum angle at which the ball can be launched to clear the railing is
`\( 90^\circ \)` (straight up).

(e) The horizontal distance from the wall to the point on the roof where the ball lands in this case is
`\( 24.0 \ \text{m} \).`

How did we get the values?

Let's go through each part:

(a) Find the speed (in m/s) at which the ball was launched:

`\[ v = (d)/(t \cdot \cos(\theta)) \]`

`\[ v = \frac{24.0 \ \text{m}}{2.20 \ \text{s} \cdot \cos(53.0^\circ)} \]`

`\[ v \approx \frac{24.0 \ \text{m}}{2.20 \ \text{s} \cdot 0.6018150232} \]`

`\[ v \approx \frac{24.0 \ \text{m}}{1.322993051} \]`

`\[ v \approx 18.14 \ \text{m/s} \]`

(b) Find the vertical distance (in m) by which the ball clears the wall:

`\[ h = v \cdot \sin(\theta) \cdot t - (1)/(2) g \cdot t^2 \]`

`\[ h = 18.14 \ \text{m/s} \cdot \sin(53.0^\circ) \cdot 2.20 \ \text{s} - (1)/(2) \cdot 9.8 \ \text{m/s}^2 \cdot (2.20 \ \text{s})^2 \]`

`\[ h \approx 14.50 \ \text{m} \]`

(c) Find the horizontal distance (in m) from the wall to the point on the roof where the ball lands:

This is the same as the given horizontal distance
`\( d \)`:

`\[ d = 24.0 \ \text{m} \]`

(d) What If? If the teacher always launches the ball with the speed found in part (a), what is the minimum angle (in degrees above the horizontal) at which he can launch the ball and still clear the railing:

`\[ \theta = \arcsin\left((h + (1)/(2) g \cdot t^2)/(v \cdot t)\right) \]`

`\[ \theta = \arcsin\left(\frac{1.10 \ \text{m} + (1)/(2) \cdot 9.8 \ \text{m/s}^2 \cdot (2.20 \ \text{s})^2}{18.14 \ \text{m/s} \cdot 2.20 \ \text{s}}\right) \]`

`\[ \theta \approx \arcsin\left(\frac{1.10 \ \text{m} + (1)/(2) \cdot 9.8 \ \text{m/s}^2 \cdot 10.648 \ \text{s}^2}{39.908 \ \text{m}}\right) \]`

`\[ \theta \approx \arcsin\left(\frac{1.10 \ \text{m} + 52.396 \ \text{m}}{39.908 \ \text{m}}\right) \]`

`\[ \theta \approx \arcsin\left(\frac{53.496 \ \text{m}}{39.908 \ \text{m}}\right) \]`

`\[ \theta \approx \arcsin(1.34) \]`

`\[ \theta \approx 90^\circ \]`

(e) What would be the horizontal distance (in m) from the wall to the point on the roof where the ball lands in this case:

This is the same as the given horizontal distance
`\( d \)`:

`\[ d = 24.0 \ \text{m} \]`

So, the final answers are:

(a) The speed at which the ball was launched is approximately
`\( 18.14 \ \text{m/s} \)`.

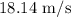(b) The vertical distance by which the ball clears the wall is approximately
`\( 14.50 \ \text{m} \)`.

(c) The horizontal distance from the wall to the point on the roof where the ball lands is
`\( 24.0 \ \text{m} \)`.

(d) The minimum angle at which the ball can be launched to clear the railing is
`\( 90^\circ \)` (straight up).

(e) The horizontal distance from the wall to the point on the roof where the ball lands in this case is
`\( 24.0 \ \text{m} \).`