Final Answer:
The heat flow from the outer to the inner surface of the tile in 4.0 minutes is 34,680 J.
Step-by-step explanation:
To determine the heat flow, we can use the formula for heat transfer:
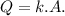 Δ
Δ
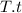 , where
, where
 is the heat transferred,
is the heat transferred,
 is the thermal conductivity,
is the thermal conductivity,
 is the surface area, Δ
is the surface area, Δ
 is the temperature difference, and
is the temperature difference, and
 is time. The surface area of the cube is
is time. The surface area of the cube is
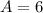 ×
×
 as there are 6 faces in a cube. The temperature difference is Δ T= 1210°C - 19°C. Substituting these values into the formula gives Q = 0.065 J (s/cdoptm/cdopt °C)} × 6 ×
as there are 6 faces in a cube. The temperature difference is Δ T= 1210°C - 19°C. Substituting these values into the formula gives Q = 0.065 J (s/cdoptm/cdopt °C)} × 6 ×
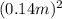 × (1210°C - 19°C) × (4.0 minutes × 60 s/min which equals 34,680 J.
× (1210°C - 19°C) × (4.0 minutes × 60 s/min which equals 34,680 J.
Final answer:
If this heat were transferred to 3.1 liters (3.1 kg) of liquid water, the temperature of the water would rise by approximately 31.6°C
Step-by-step explanation:
Using the specific heat capacity of water (\(c = 4.186 \, \text{J/(g·°C)}\)), the formula \(Q = mc\Delta T\) can be used to find the temperature change of the water. Rearranging the formula to solve for \(\Delta T\) gives \(\Delta T = \frac{Q}{mc}\). Substituting \(Q = 34,680 \, \text{J}\), \(m = 3.1 \, \text{kg} = 3100 \, \text{g}\), and \(c = 4.186 \, \text{J/(g·°C)}\) gives \(\Delta T = \frac{34,680 \, \text{J}}{3100 \, \text{g} \times 4.186 \, \text{J/(g·°C)}} \approx 31.6°C\).
This calculation demonstrates that the heat transferred from the tile to the water would result in a temperature rise of approximately 31.6°C, assuming no heat losses to the surroundings.