Question

The base of the mountain is 6,500 feet above sea level and AB measures 230 feet across. Given that the measurements for QAP is 20° and QBP is 35°, how far above sea level is peak P ? Express your answer to the nearest foot.

Height above sea level:

Answer 1

6610

Explanation:

We have tan(X) = opposite/ adjacent

tan(QBP) = PQ/BQ

tan(35) = PQ/BQ ---eq(1)

tan(QAP) = PQ/AQ

tan(20) =
`(PQ)/(AB +BQ)`

`=(1)/((AB+BQ)/(PQ) ) \\\\=(1)/((AB)/(PQ) +(BQ)/(PQ) ) \\\\= (1)/((230)/(PQ) + tan(35)) \;\;\;(from\;eq(1))\\\\= (1)/((230 + PQ tan(35))/(PQ) ) \\\\= (PQ)/(230+PQ tan(35))`

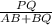
230*tan(20) + PQ*tan(20)*tan(35) = PQ

⇒ 230 tan(20) = PQ - PQ*tan(20)*tan(35)

⇒ 230 tan(20) = PQ[1 - tan(20)*tan(35)]

`PQ = (230 tan(20))/(1 - tan(20)tan(35))`

`= (230*0.36)/(1 - 0.36*0.7)\\\\= (82.8)/(1-0.25) \\\\=(82.8)/(0.75) \\\\= 110.4`

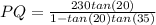
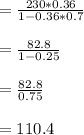
PQ = 110.4

≈110

Height above sea level = 6500 + PQ

6500 + 110

= 6610