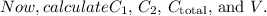Final Answer:
The capacitance of the plane is
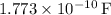 , the capacitance of the needle tip is
, the capacitance of the needle tip is
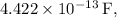 and the potential across the combination is
and the potential across the combination is

Explaination:
To model the process of charge leakage in the given scenario, we can use the concept of capacitance and potential. The capacitance
 of a conducting sphere is given by:
of a conducting sphere is given by:
![\[ C = 4\pi\epsilon_0 \left( (r_1 r_2)/(r_1 + r_2) \right) \]](https://img.qammunity.org/2024/formulas/physics/high-school/rj2s2oi6kw6lwa08b3c1ycqcdp25kinr0l.png)
where:
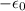 is the vacuum permittivity, approximately
is the vacuum permittivity, approximately
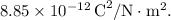
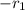 is the radius of the first sphere (representing the plane).
is the radius of the first sphere (representing the plane).
 is the radius of the second sphere (representing the tip of the needle).
is the radius of the second sphere (representing the tip of the needle).
The potential
 across a capacitor with charge
across a capacitor with charge
 and capacitance
and capacitance
 is given by:
is given by:
![\[ V = (Q)/(C) \]](https://img.qammunity.org/2024/formulas/physics/high-school/hvc0p0hx79fz378p9vwz20kwcc9qyuf9bs.png)
Now, let's calculate the capacitance of each sphere and the potential across the combination.
1. Capacitance of the plane (\( C_1 \)):
![\[ C_1 = 4\pi\epsilon_0 \left( (r_1^2)/(r_1 + r_2) \right) \]](https://img.qammunity.org/2024/formulas/physics/high-school/mdnkxwutesku84f8fqka3l0eqp1wwyer1r.png)
2. Capacitance of the needle tip
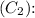
![\[ C_2 = 4\pi\epsilon_0 \left( (r_1 r_2)/(r_1 + r_2) \right) \]](https://img.qammunity.org/2024/formulas/physics/high-school/tu3jjao5d983q3zvtu7lvmww4klr10v87o.png)
3. Total capacitance

![\[ C_{\text{total}} = C_1 + C_2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/1on78nykr4g8z4x7lao1eq4rg8np68o2a5.png)
4. Potential across the combination
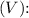
![\[ V = \frac{Q}{C_{\text{total}}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/s66y7ulip55g4fdbpv0o83tr6qv15yl7ic.png)
Let's substitute the given values into these equations:
![\[ r_1 = 6.00 \, \text{m} \]\[ r_2 = 0.02 \, \text{m} \]\[ Q = 71.0 * 10^(-6) \, \text{C} \]](https://img.qammunity.org/2024/formulas/physics/high-school/vjtyqsudx2t9a7fnr2ued2fplb3nwdpbll.png)