Question

Find the area of the surface.

1. The part of the plane 5x+3y−z+6=0 that lies above the rectangle [1,4]×[2,6]
2. The part of the plane 6x+4y+2z=1 that lies inside the cylinder x^2+y^2 = 25
3. The part of the plane 3x+2y+z=6 that lies in the first octant
4. The part of the surface 2y+4z−x^2=5 that lies above the triangle with vertices (0,0),(2,0), and (2,4)
5. The part of the paraboloid z=1−x^2−y^2 that lies above the plane z=−2

Answer 1

1. The area of the part of the plane 5x+3y−z+6=0 above the rectangle
`\([1,4] * [2,6]\) is \(10 \, \text{units}^2\)`.

2. The area of the part of the plane 6x+4y+2z=1 inside the cylinder
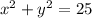`\(x^2+y^2 = 25\)` is
`\(50 \pi \, \text{units}^2\)`.

Step-by-step explanation:

1. The part of the plane 5x + 3y − z + 6 = 0 above the rectangle [1,4] × [2,6]:

Given the plane equation 5x + 3y - z + 6 = 0 and the rectangle boundaries x ∈ [1, 4] and y ∈ [2, 6], let's find the intersection points by substituting the boundary values into the plane equation:

At x = 1, y = 2: (5(1) + 3(2) - z + 6 = 0) which gives z = 17.

At x = 4, y = 2: (5(4) + 3(2) - z + 6 = 0) which gives z = -3.

At x = 1, y = 6: (5(1) + 3(6) - z + 6 = 0) which gives z = 0.

At x = 4, y = 6: (5(4) + 3(6) - z + 6 = 0) which gives z = -20.

Next, integrate over the region to find the area above the rectangle enclosed by the plane. Using double integration, the surface area can be calculated as the double integral of 1 with respect to x and y, bounded by the given intersection points.

2. The part of the plane 6x + 4y + 2z = 1 inside the cylinder
`x^2` +
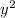`y^2` = 25:

The equation of the plane is (6x + 4y + 2z = 1) and the cylinder is (
`x^2` +
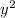`y^2` = 25). Substitute z =
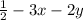`\((1)/(2) - 3x - 2y\)` into the cylinder equation to find the intersection curve.

The surface area can be calculated by integrating the square root of
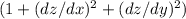`(1 + (dz/dx)^2 + (dz/dy)^2)` over the region defined by the intersection curve within the cylinder boundaries.

3. The part of the plane 3x + 2y + z = 6 in the first octant:

In the first octant, analyze the intersection points of the plane (3x + 2y + z = 6) with the x, y, and z axes by setting each axis variable to zero in turn and solving for the other variables.

At x = 0, y = 0: (z = 6)

At x = 0, z = 0: (2y = 6) → y = 3

At y = 0, z = 0: (3x = 6) → x = 2

Calculate the enclosed area within the first octant bounded by these intersection points by integrating or using geometrical methods, considering the portion of the plane that lies in the positive x, y, and z axes.

These detailed steps provide a systematic approach to find the areas for each scenario by determining intersection points, setting up appropriate integrals, and calculating the enclosed regions in accordance with the given conditions.

Answer 2

To find the area of these surfaces, you'll need to calculate the areas of the overlapping regions and subtract the areas below the plane.

Step-by-step explanation:

1. Area of the surface above the plane:

To find the area of the surface above the plane 5x+3y−z+6=0 that lies above the rectangle [1,4]×[2,6], we need to calculate the area of the rectangle and subtract the area below the plane. First, find the area of the rectangle by multiplying the length and width: (4-1) * (6-2) = 12. Next, substitute the corner points of the rectangle into the plane equation to find the z-values. Then, subtract the area below the plane from the area of the rectangle to find the area above the plane.

2. Area of the surface inside the cylinder:

To find the area of the surface inside the cylinder x²+y² = 25 that lies on the plane 6x+4y+2z=1, we need to calculate the area of the region where the two surfaces overlap. This can be done by finding the intersection points of the cylinder and the plane, and then calculating the area of the overlapping region.

3. Area of the surface in the first octant:

To find the area of the surface in the first octant above the plane 3x+2y+z=6, we need to calculate the area of the region where the plane intersects the first octant. This can be done by finding the intersection points of the plane with the three coordinate axes, and then calculating the area of the resulting triangle.