Question

What is the phase angle ϕ for the source voltage relative to the current? Express your answer in degrees. A capacitor is connected across an ac source that has voltage amplitude 64.0 V and frequency 75.5 Hz. Part B Does the source voltage lag or lead the current? What is the capacitance C of the capacitor if the current amplitude is 5.35 A ? Express your answer with the appropriate units.

Answer 1

When a sinusoidal voltage is applied to a capacitor, the voltage follows the current by 90° phase angle. The source voltage lags the current in this case. The capacitance C of the capacitor can be calculated using the formula C = I / (2πfV).

Step-by-step explanation:

When a sinusoidal voltage is applied to a capacitor, the voltage follows the current by one-fourth of a cycle, or by a 90° phase angle. In this case, since the question mentions a capacitor connected across an AC source, we can infer that the voltage across the capacitor lags the current. Therefore, the source voltage lags the current.

The capacitance C of the capacitor can be calculated using the formula:

C = I / (2πfV)

Where I is the current amplitude, f is the frequency, and V is the voltage amplitude. Substituting the given values, we have:

C = 5.35 A / (2π * 75.5 Hz * 64.0 V)

Simplifying the expression yields the value of the capacitance C.

Answer 2

The capacitance (C) of the capacitor is approximately
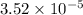`\(3.52 * 10^(-5)\)` Farads (F).

To find the phase angle
`(\( \phi \))` between the source voltage and the current in a capacitive circuit, you can use the relationship between voltage
`(\( V \))`, current
`(\( I \))`, and the capacitive reactance
`(\( X_C \))`:

The voltage across a capacitor in an AC circuit leads the current by a phase angle of 90 degrees in a capacitive circuit.

Given:

Voltage amplitude (V) = 64.0 V

Frequency ( f ) = 75.5 Hz

Current amplitude ( I ) = 5.35 A

First, let's determine the phase angle (
`\( \phi \)`):

`\[ \phi = 90^\circ \]`

The source voltage leads the current by 90 degrees in a capacitive circuit.

Regarding whether the source voltage lags or leads the current: In a capacitive circuit, the source voltage leads the current.

Now, to find the capacitance (C) of the capacitor, we can use the relationship between capacitive reactance
`(\( X_C \))`, capacitance ( C ), and frequency ( f ) in an AC circuit:

`\[ X_C = (1)/(2 \pi f C) \]`

Given that the current amplitude ( I ) = 5.35 A and the voltage amplitude ( V ) = 64.0 V, the capacitive reactance
`(\( X_C \))` is related to the current and voltage as:

`\[ X_C = (V)/(I) \]`

Substitute the values to find
`\( X_C \)`:

`\[ X_C = \frac{64.0 \, \text{V}}{5.35 \, \text{A}} \]`

`\[ X_C \approx 11.972 \, \Omega \]`

Now, using the formula for capacitive reactance:

`\[ X_C = (1)/(2 \pi f C) \]`

`\[ C = (1)/(2 \pi f X_C) \]`

`\[ C = \frac{1}{2 \pi * 75.5 \, \text{Hz} * 11.972 \, \Omega} \]`

`\[ C \approx 3.52 * 10^(-5) \, \text{F} \]`