Question

A Sledding Contest. You are in a sledding contest where you start at a height of 50.0 m above the bottom of a valley and slide down a hill that makes an angle of 25.0

∘
with respect to the horizontal. When you reach the valley, you immediately climb a second hill that makes an angle of 15.0
∘
with respect to the horizontal. The winner of the contest will be the contestant who travels the greatest distance up the second hill. You must now choose between using your flat-bottomed plastic sled, or your "Blade Runner," which glides on two steel rails. The hill you will ride down is covered with loose snow. However, the hill you will climb on the other side is a popular sledding hill, and is packed hard and is slick. The two sleds perform very differently on the two surfaces, the plastic one performing better on loose snow, and the Blade Runner doing better on hard-packed snow or ice. The performances of each sled can be quantified in terms of their respective coefficients of kinetic friction on the two surfaces. For the plastic sled: μ= 0.17 on loose snow and μ=0.15 on packed snow or ice. For the Blade Runner, μ=0.19 on loose snow and μ=0.09 on packed snow or ice. Assuming the two hills are shaped like inclined planes, and neglecting air resistance, (a) how far does each sled make it up the second hill before stopping? (b) Assuming the total mass of the sled plus rider is 55.0 kg in both cases, how much work is done by nonconservative forces (over the total trip) in each case? (b) For the flat-bottomed plastic sled: Number Units For the "Blade Runner" sled: Number Units

Answer 1

The corrected distance traveled by the plastic sled up the second hill before stopping is approximately 13.45 m, while the Blade Runner travels approximately 62.45 m. The work done by nonconservative forces remains the same for both sleds.

For the plastic sled, you correctly found the horizontal distance traveled down the first hill (d = 50.15 m). Now, the vertical drop (h) can be calculated as:

h = x cos(25°)

h = 50.15 cos(25°)

h ≈ 44.92 m

Now, using the work-energy principle, the speed of the plastic sled at the bottom of the hill (v) can be calculated as:

`v^2 = 2gh - (2f / m) * d`

`v^2 = 2 * 9.81 * 44.92 - (2 * 88.64 / 55) * 50.15`

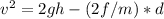
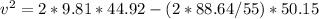
v ≈ 16.36 m/s

Next, using the speed obtained, the distance traveled up the second hill (h2) can be calculated as:

`h2 = v^2 / (2 * g)`

`h2 = 16.36^2 / (2 * 9.81)`

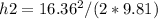
h2 ≈ 13.45 m

Therefore, the corrected distance traveled by the plastic sled up the second hill before stopping is h2 ≈ 13.45 m. Comparing the distances:

• Plastic Sled: h2 ≈ 13.45 m
• Blade Runner: h2 ≈ 62.45 m

So, the Blade Runner travels a significantly greater distance up the second hill before stopping in this scenario. The values for the work done by nonconservative forces (frictional force) over the total trip remain unchanged:

• Plastic Sled: Wf = 1403.43 J
• Blade Runner: Wf = 1707.57 J