Question

A particle moves according to the following equation: x=0.2cos( 2π​t+ 2π ) : a) What is the position of the particle when t=0 s? b) What is the speed of the particle when t=0 s? c) What is the speed of the particle when t=3s ?

Answer 1

Explanation:

Given the position function, plug in 0 for t to find it's position

`x = 0.2 \cos(2\pi)`

`x (0) = 0.2`

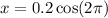
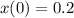
So the position at t=0 is 0.2 units

B. Take the derivative of position function

to get the speed.

`(d)/(dx) (0.2 \cos(2\pi + 2\pi)`

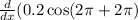
Use the chain rule

`- 0.2 \sin(2t\pi + 2\pi ) * 2\pi`

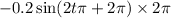
Which simplifies to

`- 0.4 \sin(2t\pi + 2\pi)`

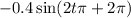
Plug in 0 for t to find the speed.

`- 0.4 \sin(2\pi) = 0`

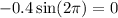
So B is 0 units/seconds.

C.

Plug in. 3 for t in the derivative function

`- 0.4 \sin(8\pi) = 0`

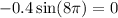
8pi reference angle is 0, so the speed is 0 as well

So C is 0 units/seconds