Question

find the equation of the locus of amoving point which moves that it is equidistant from two fixed points (2,4) and (-3,-2)​

Answer 1

`10x+12y=7`

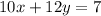
Explanation:

Let the moving point be P(x, y).

The distance between P and (2, 4) is:

`√((x - 2)^2 + (y - 4)^2)`

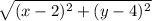
The distance between P and (-3, -2) is:

`√((x + 3)^2 + (y + 2)^2)`

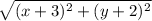
Since P is equidistant from (2, 4) and (-3, -2), the two distances are equal.

`√((x - 2)^2 + (y - 4)^2) = √((x + 3)^2 + (y + 2)^2)`

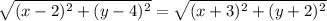
Squaring both sides of the equation, we get:

`(x - 2)^2 + (y - 4)^2 = (x + 3)^2 + (y + 2)^2`

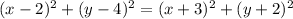
Expanding the terms on both sides of the equation, we get:

`x^2-4x+4 + y^2 - 8y + 16 = x^2 + 6x + 9 + y^2+ 4y +4`

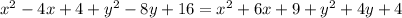
Simplifying both sides of the equation, we get:

`x^2-4x+4 + y^2 - 8y + 16 = x^2 + 6x + 9 + y^2+ 4y +4`

`x^2-x^2-4x-6x+y^2-y^2-8y-4y+4+16-9-4=0`

`-10x - 12y + 7= 0`

`10x+12y=7`

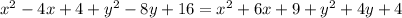
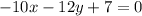
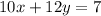
This is the equation of the locus of the moving point.