Question

Solve the quadratic equation by using the square root property.
(2x + 3)2 = 81

Answer 1

Answer: x = 3 and x = -6

Explanation:

the first step is to square root both sides of the equation to get rid of the exponent (2) on the left side of the equation, however lets break it down:

`(2x + 3)^2 = 81\\\\`

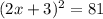
81 can be rewritten as 9^2

`(2x + 3)^2= 9^2`

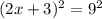
and now lets square root both sides:

`√((2x+3)^2) =√(9^2)`

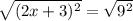
The squares (the exponent 2) cancels out with the square root:

2x + 3 = +/- 9

now lets isolate x by subtracting 3 from both sides:

2x + 3 = +/- 9

-3 -3

2x = -3 +/- 9

2x = -3 + 9

2x = 6

2x = -3 - 9

2x = 12

And after simplifying, you can divide two on both sides:

2x = 6

/2 /2

x = 3

2x = -12

/2 /2

x = -6

x = 3 and x = -6