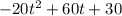Question

Find the position and velocity of an object moving along a straight line with the given acceleration, initial velocity, and initial position. a(t)=−40,v(0)=60, and s(0)=30 v(t) = ___ s(t) = ___

Answer 1

s(t) = -20t^2 + 60t + 30

v(t) = -40t + 60

Explanation:

This problem relies on the knowledge that acceleration is the derivative of velocity and velocity is the derivative of position. If calculus is not required for this problem yet, the same theory applies. Acceleration is the change in velocity with respect to time, and velocity is the change in position with respect to time.

a(t) =
`(dv)/(dt)`

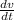
a(t) *dt = dv

`\int{dv}` =
`\int{a(t)} dt` =
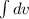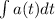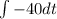`\int{-40}dt`, where the integral is evaluated from t(0) to some time t(x).

v(t) = -40t+ C, where C is a constant and is equal to v(0).

v(t) = -40t + 60

v(t) =
`(ds)/(dt)`

`(ds)/(dt)` = -40t+60

ds = (-40t+60) dt

`\int ds` =
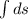`\int{-40t dt}`, where the integral is evaluated from t(0) to the same time t(x) as before.

s(t) =
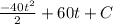`(-40t^2)/(2)+60t+C`, where C is a different constant and is equal to s(0).

s(t) =
`-20t^2+60t+30`