Question

NO LINKS!! URGENT HELP PLEASE!!!

9. Find the equation of the PARABOLA with a vertex at (-2, 6) and passing through the point (1, -3)

Answer 1

y= -x²-4x+2

Explanation:

write in vertex form

a(x-h)²+k

in our case h = -2 and k= 6

y=a(x+2)²+6

now we just need to solve for a. we know that when x= 1 y = -3. plug these values in and solve for a

-3= a(1+2)²+6

-9=9a

a= -1

thus the formula is -(x+2)²+6

generally, teachers want things in standard form, so expand the exponent and simplify.

-(x²+4x+4)+6

y= -x²-4x+2

Answer 2

`y = -x^2 - 4x + 2`

Explanation:

The equation of a parabola in vertex form is:

`y = a(x - h)^2 + k`

where (h, k) is the vertex of the parabola.

In this case, the vertex is (-2, 6), so h = -2 and k = 6.

We also know that the parabola passes through the point (1, -3).

Plugging these values into the equation, we get:

`-3 = a(1 - (-2))^2 + 6`

`-3 = a(3)^2 + 6`

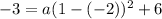
-9 = 9a

a = -1

Substituting a = -1 into the equation for a parabola in vertex form, we get the equation of the parabola:

`y = -1(x + 2)^2 + 6`

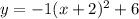
This equation can also be written as:

`y = -x^2 - 4x -4+6\\y=x^2-4x+2`