Question

NO LINKS!! URGENT HELP PLEASE!!!

10. Find the equation of the circle below.​

Answer 1

(x+3)^2 + (y+1)^2 = 16

Explanation:

The equation of a circle is (x – h)^2 + (y – k)^2 = r^2, where h is the x value of the center, k is the y value of the center, and r is the radius.

We can see from the picture that the radius is at about (-3, -1) and the radius is about 4, so we can plug those in:
(x – (-3))^2 + (y – (-1))^2 = 4^2

Simplify:
(x+3)^2 + (y+1)^2 = 16

Answer 2

Equation of circle:
`(x + 3)^2 + (y + 1)^2 = 16`

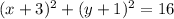
Explanation:

Given:

Center of the circle = (-3, -1)

Point on the circle = (1, -1)

In order to find the radius of the circle, we can use the distance formula.

distance =
`\boxed{\bold{√((x_1 - x_2)^2 + (y_1 - y_2)^2)}}`

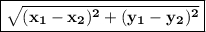
where:

• x1 and y1 are the coordinates of the center of the circle
• x2 and y2 are the coordinates of the point on the circle

In this case, the distance formula becomes:

radius =
`√((-3 - 1)^2 + ((-1) - (-1))^2)= √(16)=4`

Therefore, the radius of the circle is 4 units.

Now that we know the radius of the circle, we can find the equation of the circle using the following formula:

`\boxed{\bold{(x - h)^2 + (y - k)^2 = r^2}}`

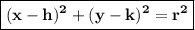
where:

• h and k are the coordinates of the center of the circle
• r is the radius of the circle

In this case, the equation of the circle becomes:

=
`(x + 3)^2 + (y + 1)^2 = 4^2`

=
`(x + 3)^2 + (y + 1)^2 = 16`

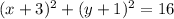
This is the equation of the circle.