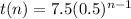Question

NO LINKS!! URGENT HELP PLEASE!!!

9. a. Finish the table
b. Name the type of sequence
c. Find an equation for the following sequence
​

Answer 1

`\textsf{a.}\quad \begin{array}c\cline{1-6}\vphantom{\frac12} n&1&2&3&4&5\\\cline{1-6}\vphantom{\frac12}t(n)&7.5&3.75&1.875&0.9375&0.4687\\\cline{1-6}\end{array}`

`\textsf{b.} \quad \textsf{Geometric sequence.}`

`\textsf{c.} \quad t(n)=7.5(0.5)^(n-1)`

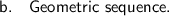
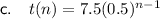
Explanation:

Before we can complete the table, we need to determine if the sequence is arithmetic or geometric.

To determine if a sequence is arithmetic or geometric, examine the pattern of the terms in the sequence.

• In an arithmetic sequence, the difference between consecutive terms (called the common difference) remains constant.
• In a geometric sequence, the ratio between consecutive terms (called the common ratio) remains constant.

Calculate the difference between consecutive terms by subtracting one term from the next:

`t(2)-t(1)=3.75-7.5=-3.75`

`t(3)-t(2)=1.875-3.75 = -1,875`

As the difference is not common, the sequence is not arithmetic.

Calculate the ratio between consecutive terms by dividing one term by the previous term.

`(t(2))/(t(1))=(3.75)/(7.5)=0.5`

`(t(3))/(t(2))=(1.875)/(3.75)=0.5`

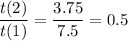
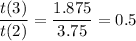
As the ratio is common, the sequence is geometric.

To complete the table, multiply the preceding term by the common ratio 0.5 to calculate the next term:

`t(4)=t(3) * 0.5=1.875 * 0.5=0.9375`

`t(5)=t(4) * 0.5=0.9375 * 0.5=0.46875`

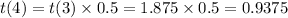
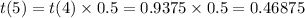
Therefore, the completed table is:

`\begin{array}\cline{1-6}\vphantom{\frac12} n&1&2&3&4&5\\\cline{1-6}\vphantom{\frac12}t(n)&7.5&3.75&1.875&0.9375&0.4687\\\cline{1-6}\end{array}`

To find an equation for the sequence, use the general form of a geometric sequence:

`\boxed{\begin{minipage}{5.5 cm}\underline{Geometric sequence}\\\\$a_n=ar^(n-1)$\\\\where:\\\phantom{ww}$\bullet$ $a$ is the first term. \\\phantom{ww}$\bullet$ $r$ is the common ratio.\\\phantom{ww}$\bullet$ $a_n$ is the $n$th term.\\\phantom{ww}$\bullet$ $n$ is the position of the term.\\\end{minipage}}`

In this case, the first term is the value of t(n) when n = 1, so a = 7.5

We have already calculated the common ratio as being 0.5, so r = 0.5.

Substitute these values into the formula to create an equation for the sequence:

`t(n)=7.5(0.5)^(n-1)`

Answer 2

a. 0.9375, 0.46875

b. geometric sequence

c. equation:
`7.5 * ((1)/(2))^(n-1)`

Explanation:

a.

The table can be finished as follows:

n t(n)

1 7.5

2 3.75

3. 1.875

4. 0.9375

5 0.46875

b.

The type of sequence is a geometric sequence.

A geometric sequence is a sequence of numbers where the ratio between any two consecutive terms is constant.

In this case, the ratio between any two consecutive terms is 3.75/7.5=½ ,

so the sequence is geometric.

c.

The equation for the sequence is t(n) = 7.5 * (1/2)^n.

This equation can be found by looking at the first term of the sequence (7.5) and the common ratio (1/2).

t(1) = 7.5

t(2) = 7.5 * (1/2) = 3.75

t(3) = 7.5 * (1/2)^2 = 1.875

The equation can also be found by looking at the general formula for a geometric sequence,

which is
`t(n) = a*r^(n-1)`

In this case,

• a = 7.5
• r = 1/2.

t(n) =
`7.5 * ((1)/(2))^(n-1)`

This is the required equation.