Question

100 Points! Geometry question. Determine whether each pair of triangles is similar. If so, write a similarity statement. If not, what would be sufficient to prove the triangles similar? Explain your reasoning. Photo attached. Thank you!

Answer 1

ΔABC ~ ΔPQR

Explanation:

In similar triangles, corresponding sides are always in the same ratio.

Therefore, if triangle ABC is similar to triangle PQR then:

`AB : PQ = BC : QR = AC : PR`

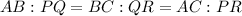
Substitute the side lengths into the ratio equation:

`AB : PQ = BC : QR = AC : PR`

`8 : 6 \;\;\;\:= \;\;12 : 9 \;\;\;\:= \;\;12 : 9`

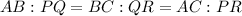
Simplify each ratio by dividing all parts of the ratio by their highest common factor:

`(8)/(2):(6)/(2)=(12)/(3):(9)/(3)=(12)/(3):(9)/(3)`

`4:3=4:3=4:3`

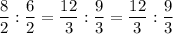
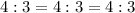
As the corresponding sides of triangles ABC and PQR are in the same ratio, this proves that the two triangles are similar.

Answer 2

Δ ABC
`\bold{\sim}` ΔPQR is similar.

Explanation:

Similar triangles are two or more triangles that have the same shape, but their sides are in proportion.

For Question:

In Δ ABC and ΔPQR

AB:PQ =8:6=4:3

BC: QR=12:9=4:3

AC: PR=12:9=4:3

Since the length of any side of one triangle is by the corresponding side of another triangle, you will get the same number.

Therefore,

Δ ABC
`\bold{\sim}` ΔPQR is similar.

Hence Proved: