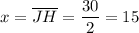Answer:
x = 15
Explanation:
The midsegment of a triangle is a line segment that connects the midpoints of two sides of a triangle.
Therefore, if JH is the midsegment of ΔKLM then JH is parallel to LM, and triangles KJH and KLM are similar: ΔKJH ~ ΔKLM.
In similar triangles, corresponding sides are always in the same ratio.
Since JH is the midsegment of ΔKLM, then KJ is half the length of KL, and KH is half the length of KM. This means that JH is half the length of LM.
Given the measure of LM is 30: