Answer:
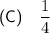
Explanation:
To find the probability of a point chosen at random being in the shaded area of the given diagram, we first need to calculate the areas of the larger circle and the shaded circle.
The formula for the area of a circle is A = πr², where r is the radius.
Given the radius of the larger circle is 8 units:
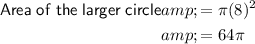
Given the radius of the shaded circle is 4 units:
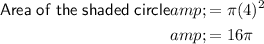
Probability formula
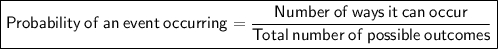
To find the probability that a point chosen at random is in the shaded area, divide the area of the shaded circle by the area of the larger circle:
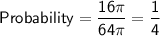
Therefore, the probability of a point chosen at random being in the shaded area is 1/4.