Question

figure 5.28 shows a 5.0 kg block a being pushed with a 3.0 n force. in front of this block is a 10 kg block b; the two blocks move together. what force does block a exert on block b?

Answer 1

In a scenario where block A is pushing block B and no friction or resistive forces are considered, block A would exert the same force on block B as is applied to it, which is 3.0 N.

Step-by-step explanation:

The question asks about the force that block A exerts on block B when a 3.0 N force is applied to block A and it pushes block B. Since the blocks move together, and friction is not mentioned, we assume a frictionless surface for simplicity. According to Newton's Third Law of Motion, every action has an equal and opposite reaction. Therefore, the force block A exerts on block B will be equal to the force applied to it minus any force lost due to friction or other resistive forces. If friction is neglected or is zero, block A would exert a force of 3.0 N on block B, the same as the pushing force.

Answer 2

The force exerted by Block A on Block B is 2.0 Newtons.

To calculate the force exerted by Block A on Block B, you can use Newton's third law of motion, which states that action and reaction forces are equal and opposite.

Given:

Force applied on Block A (F) = 3.0 N (applied force)

Mass of Block A
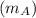`(m_A)` = 5.0 kg

Mass of Block B
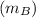`(m_B)` = 10 kg

The force exerted by Block A on Block B is the same as the force that causes both blocks to move together.

Acceleration of the system:

`\[ \text{Acceleration} = \frac{\text{Net Force}}{\text{Total Mass}} \]`

The net force acting on the system is the force applied to Block A:

`\[ \text{Net Force} = F = 3.0 \, \text{N} \]`

Total mass of the system:

`\[ \text{Total Mass} = m_A + m_B = 5.0 \, \text{kg} + 10 \, \text{kg} = 15.0 \, \text{kg} \]`

Now, calculate the acceleration:

`\[ \text{Acceleration} = \frac{F}{\text{Total Mass}} = \frac{3.0 \, \text{N}}{15.0 \, \text{kg}} = 0.2 \, \text{m/s}^2 \]`

Since the blocks move together, the force exerted by Block A on Block B can also be found using Newton's second law:

`\[ \text{Force} = \text{mass} * \text{acceleration} \]`

`\[ \text{Force} = m_B * \text{Acceleration} = 10 \, \text{kg} * 0.2 \, \text{m/s}^2 = 2.0 \, \text{N} \]`