Question

100 Points! Geometry question. Photo attached. Find the measure. Please show as much work as possible. Thank you!

Answer 1

Explanation:

The inscribed angle MPN intercepts twice as many degrees of arc as its measure

so MN = 62 degrees

the lower NP is 180 degrees

the remainder of the 360 degree circle is MP

360 - 180 - 62 = MP = 118 degrees

Answer 2

`m\overset\frown{MP} =118^(\circ)`

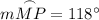
Explanation:

The diagram shows a circle with an inscribed angle NPM and an intercepted arc NM.

To find the measure of arc MP, we first need to find the measure of the intercepted arc NM.

According to the Inscribed Angle Theorem, the measure of an inscribed angle is half the measure of the intercepted arc. Therefore:

`m \angle NPM = (1)/(2) \overset\frown{NM}`

`31^(\circ) = (1)/(2) \overset\frown{NM}`

`\overset\frown{NM}=62^(\circ)`

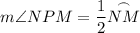
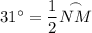
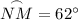
The minor arcs in a semicircle sum to 180°. Therefore:

`\overset\frown{MP} + \overset\frown{NM} = 180^(\circ)`

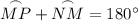
Substitute the found measure of arc MN into the equation:

`\overset\frown{MP} +62^(\circ) = 180^(\circ)`

`\overset\frown{MP} +62^(\circ) -62^(\circ)= 180^(\circ)-62^(\circ)`

`\overset\frown{MP} =118^(\circ)`

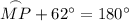
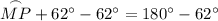
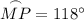
Therefore, the measure of arc MP is 118°.

`\hrulefill`

Additional information

• An inscribed angle is the angle formed (vertex) when two chords meet at one point on a circle.
• An intercepted arc is the arc that is between the endpoints of the chords that form the inscribed angle.