Question

100 Points! Geometry question. Photo attached. Please show as much work as possible. Thank you!

Answer 1

`BC=5.1`

`B=23^(\circ)`

`C=116^(\circ)`

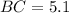
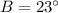
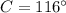
Explanation:

The diagram shows triangle ABC, with two side measures and the included angle.

To find the measure of the third side, we can use the Law of Cosines.

`\boxed{\begin{minipage}{6 cm}\underline{Law of Cosines} \\\\$c^2=a^2+b^2-2ab \cos C$\\\\where:\\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides.\\ \phantom{ww}$\bullet$ $C$ is the angle opposite side $c$. \\\end{minipage}}`

In this case, A is the angle, and BC is the side opposite angle A, so:

`BC^2=AB^2+AC^2-2(AB)(AC) \cos A`

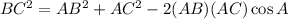
Substitute the given side lengths and angle in the formula, and solve for BC:

`BC^2=7^2+3^2-2(7)(3) \cos 41^(\circ)`

`BC^2=49+9-2(7)(3) \cos 41^(\circ)`

`BC^2=49+9-42\cos 41^(\circ)`

`BC^2=58-42\cos 41^(\circ)`

`BC=\sqrt{58-42\cos 41^(\circ)}`

`BC=5.12856682...`

`BC=5.1\; \sf (nearest\;tenth)`

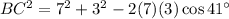
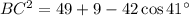
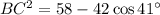
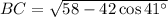
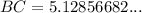
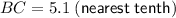
Now we have the length of all three sides of the triangle and one of the interior angles, we can use the Law of Sines to find the measures of angles B and C.

`\boxed{\begin{minipage}{7.6 cm}\underline{Law of Sines} \\\\$(\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c) $\\\\\\where:\\ \phantom{ww}$\bullet$ $A, B$ and $C$ are the angles. \\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides opposite the angles.\\\end{minipage}}`

In this case, side BC is opposite angle A, side AC is opposite angle B, and side AB is opposite angle C. Therefore:

`(\sin A)/(BC)=(\sin B)/(AC)=(\sin C)/(AB)`

Substitute the values of the sides and angle A into the formula and solve for the remaining angles.

`(\sin 41^(\circ))/(5.12856682...)=(\sin B)/(3)=(\sin C)/(7)`

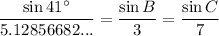
Therefore:

`(\sin B)/(3)=(\sin 41^(\circ))/(5.12856682...)`

`\sin B=(3\sin 41^(\circ))/(5.12856682...)`

`B=\sin^(-1)\left((3\sin 41^(\circ))/(5.12856682...)\right)`

`B=22.5672442...^(\circ)`

`B=23^(\circ)`

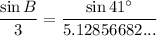
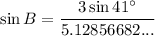
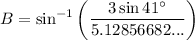
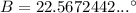
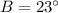
From the diagram, we can see that angle C is obtuse (it measures more than 90° but less than 180°). Therefore, we need to use sin(180° - C):

`(\sin (180^(\circ)-C))/(7)=(\sin 41^(\circ))/(5.12856682...)`

`\sin (180^(\circ)-C)=(7\sin 41^(\circ))/(5.12856682...)`

`180^(\circ)-C=\sin^(-1)\left((7\sin 41^(\circ))/(5.12856682...)\right)`

`180^(\circ)-C=63.5672442...^(\circ)`

`C=180^(\circ)-63.5672442...^(\circ)`

`C=116.432755...^(\circ)`

`C=116^(\circ)`

`\hrulefill`

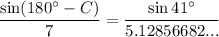
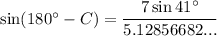
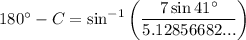
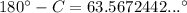
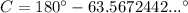
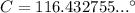
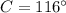
Additional notes:

I have used the exact measure of side BC in my calculations for angles B and C. However, the results will be the same (when rounded to the nearest degree), if you use the rounded measure of BC in your angle calculations.