Question

Use the definition to calculate the derivative of the following function. Then find the values of the derivative as specified.

Answer 1

Refer to the step-by-step explanation, please follow along very carefully. Answers are encased in two boxes.

Explanation:

Given the following function, find it's derivative using the definition of derivatives. Evaluate the function when θ=1, 11, and 3/11

`p(\theta)=√(11\theta)`

`\hrulefill`

The definition of derivatives states that the derivative of a function at a specific point measures the rate of change of the function at that point. It is defined as the limit of the difference quotient as the change in the input variable approaches zero.

`f'(x) = \lim_{{h \to 0}} \frac{{f(x+h) - f(x)}}{{h}}`
`\hrulefill`

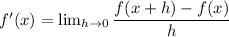
To apply the definition of derivatives to this problem, follow these step-by-step instructions:

Step 1: Identify the function: Determine the function for which you want to find the derivative. In out case the function is denoted as p(θ).

`p(\theta)=√(11\theta)`

Step 2: Write the difference quotient: Using the definition of derivatives, write down the difference quotient. The general form of the difference quotient is (f(x+h) - f(x))/h, where "x" is the point at which you want to find the derivative, and "h" represents a small change in the input variable. In our case:

`p'(\theta) = \lim_{{h \to 0}} \frac{{p(\theta+h) - p(\theta)}}{{h}}\\\\\\\Longrightarrow p'(\theta)= \lim_(h \to 0) (√(11(\theta + h)) - √(11\theta) )/(h)`

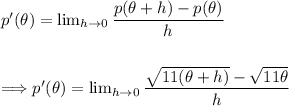
Step 3: Take the limit:

We need to rationalize the numerator. Rewriting using radical rules.

`p'(\theta)= \lim_(h \to 0) (√(11(\theta + h)) - √(11\theta) )/(h) \\\\\\\Longrightarrow p'(\theta)= \lim_(h \to 0) (√(11\theta + 11h) - √(11\theta) )/(h)\\\\\\\Longrightarrow p'(\theta)= \lim_(h \to 0) (√(11)√(\theta+h) - √(11)√(\theta) )/(h)`

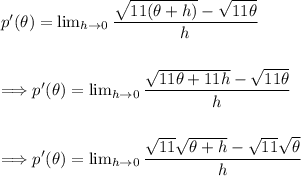
Now multiply by the conjugate.

`p'(\theta)= \lim_(h \to 0) (√(11)√(\theta+h) - √(11)√(\theta) )/(h) \cdot (√(11)√(\theta+h) + √(11)√(\theta) )/(√(11)√(\theta+h) + √(11)√(\theta) ) \\\\\\\Longrightarrow p'(\theta)= \lim_(h \to 0) ((√(11)√(\theta+h) - √(11)√(\theta) )(√(11)√(\theta+h) + √(11)√(\theta) ))/(h(√(11)√(\theta+h) + √(11)√(\theta) )) \\\\\\`

`\Longrightarrow p'(\theta)= \lim_(h \to 0) (11h)/(h(√(11)√(\theta+h) + √(11)√(\theta) ))\\\\\\\Longrightarrow p'(\theta)= \lim_(h \to 0) (11)/(√(11)√(\theta+h) + √(11)√(\theta) )`

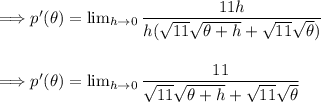
Step 4: Simplify the expression: Evaluate the limit by substituting the value of h=0 into the difference quotient. Simplify the expression as much as possible.

`p'(\theta)= \lim_(h \to 0) (11)/(√(11)√(\theta+h) + √(11)√(\theta) )\\\\\\\Longrightarrow p'(\theta)= (11)/(√(11)√(\theta+(0)) + √(11)√(\theta) )\\\\\\\Longrightarrow p'(\theta)= (11)/(√(11)√(\theta) + √(11)√(\theta) )\\\\\\\Longrightarrow p'(\theta)= (11)/(2√(11)√(\theta) )\\\\\\\Longrightarrow p'(\theta)= (11)/(2√(11\theta) )\\\\\\\Longrightarrow p'(\theta)= (11)/(2√(11\theta) )`

`\therefore \boxed{\boxed{p'(\theta)= (√(11) )/(2√(\theta) )}}`

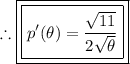
Thus, we have found the derivative on the function using the definition.

It's important to note that in practice, finding derivatives using the definition can be a tedious process, especially for more complex functions. However, the definition lays the foundation for understanding the concept of derivatives and its applications. In practice, there are various rules and techniques, such as the power rule, product rule, and chain rule, that can be applied to find derivatives more efficiently.
`\hrulefill`

Now evaluating the function at the given points.

`p'(\theta)= (√(11) )/(2√(\theta)); \ p'(1)=??, \ p'(11)=??, \ p'((3)/(11) )=??`

When θ=1:

`p'(\theta)= (√(11) )/(2√(\theta))\\\\\\\Longrightarrow p'(1)= (√(11) )/(2√(1))\\\\\\\therefore \boxed{\boxed{p'(1)= (√(11) )/(2)}}`

When θ=11:

`p'(\theta)= (√(11) )/(2√(\theta))\\\\\\\Longrightarrow p'(11)= (√(11) )/(2√(11))\\\\\\\therefore \boxed{\boxed{p'(11)= (1)/(2)}}`

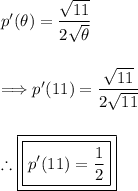
When θ=3/11:

`p'(\theta)= (√(11) )/(2√(\theta))\\\\\\\Longrightarrow p'((3)/(11) )= \frac{√(11) }{2\sqrt{(3)/(11) }}\\\\\\\therefore \boxed{\boxed{p'((3)/(11) )= (11√(3) )/(6)}}`

Thus, all parts are solved.