Answer:
The derivative of the function:
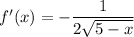
The tangent line of the function at the given point:
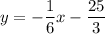
Explanation:
Find the equation of the tangent line of the given function using the given point.
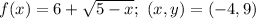

To find the equation of the tangent line to a function at a given point, follow these step-by-step instructions:
Step 1: Identify the point of tangency
- Determine the x-coordinate of the point of tangency. Let's call it x₀.
- Find the corresponding y-coordinate of the point of tangency. Let's call it y₀.
Step 2: Find the derivative of the function
- Calculate the derivative of the given function. Let's denote it as f'(x).
Step 3: Substitute the x-coordinate into the derivative
- Replace the variable x in the derivative function f'(x) with the x-coordinate of the point of tangency (x₀).
- Evaluate the derivative at x₀ to find the slope of the tangent line. Let's denote it as m.
Step 4: Write the equation of the tangent line
- Use the point-slope form of a line: y - y₀ = m(x - x₀).
- Substitute the values of m, x₀, and y₀ into the equation.
- Simplify and rearrange the equation to obtain the final form.
Step 5: Optional - Simplify the equation
- If necessary, simplify the equation by performing any algebraic manipulations.
Step 6: Optional - Verify the equation
- Check the obtained equation by plugging in other points along the tangent line and ensuring they satisfy the equation.

Step 1:
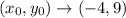
Step 2:
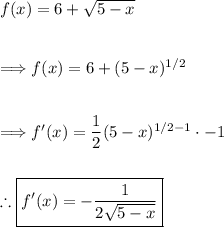
Step 3:
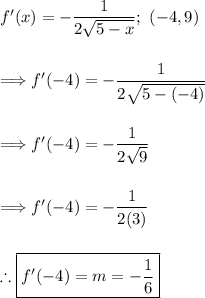
Step 4 and 5:

Thus, the problem is solved.