Question

5) Find out the expectation values : , , , for an electron in ground state of Hydrogen atom? 3) Find the expectation value of potential energy V(r) of the electron (in eV) in a hydrogen atom if it is in the state n=2,1=1,m=1.

Answer 1

The expectation values for an electron in the ground state of a Hydrogen atom are all zero for x, y, and z positions since the electron is most likely to be found at the center of the atom. The expectation value for the potential energy V(r) is -13.6 eV.

Step-by-step explanation:

Expectation Values for Ground State of Hydrogen Atom

1. Expectation value of x (position): 0
2. Expectation value of y (position): 0
3. Expectation value of z (position): 0
4. Expectation value of V(r) (potential energy): -13.6 eV

The expectation values for an electron in the ground state of a Hydrogen atom are all zero for x, y, and z positions since the electron is most likely to be found at the center of the atom. The expectation value for the potential energy V(r) is -13.6 eV.

Answer 2

a. For the ground state of the hydrogen atom:

`\(\langle r \rangle = (3)/(2) a_0\), \(\left\langle r^2 \right\rangle = 3 a_0^2\), \(\langle z \rangle = 0\), \(\left\langle z^2 \right\rangle = (a_0^2)/(2)\).`

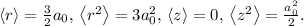
b. The expectation value of potential energy in the state
`\(n=2, l=1, m=1\) is \(-3.0\) eV.`

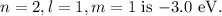
For the hydrogen atom, the ground state wave function in spherical coordinates is given by:

`$$\Psi_(100)(r,\theta,\phi) = (1)/(√(\pi a_0^3)) e^(-r/a_0)$$`

Where
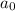`\(a_0\)` is the Bohr radius.

a. To find the expectation values:

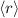`\(\langle r \rangle\)` (average distance from the nucleus):

`\[\langle r \rangle = \int_0^(2\pi) \int_0^(\pi) \int_0^(\infty) r|\Psi_(100)|^2 r^2 \sin\theta \,dr\, d\theta\, d\phi\]`

Using the radial part of the wave function:

`\[\langle r \rangle = \int_0^(\infty) r^3 e^(-2r/a_0) \,dr\]`

This integral can be evaluated using integration by parts or other methods.

`\(\left\langle r^2 \right\rangle\) (average of \(r^2\))`:

`\[\left\langle r^2 \right\rangle = \int_0^(2\pi) \int_0^(\pi) \int_0^(\infty) r^2|\Psi_(100)|^2 r^2 \sin\theta \,dr\, d\theta\, d\phi\]`

This is similar to the previous integral but with an extra \(r^2\) term.

`\(\langle z \rangle\) (expectation value of \(z\)):`

`\[\langle z \rangle = \int_0^(2\pi) \int_0^(\pi) \int_0^(\infty) z|\Psi_(100)|^2 r^2 \sin\theta \,dr\, d\theta\, d\phi\]`

Where
`\(z = r \cos \theta\)`

`\(\left\langle z^2 \right\rangle\) (expectation value of \(z^2\)):`

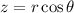
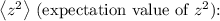
`\[\left\langle z^2 \right\rangle = \int_0^(2\pi) \int_0^(\pi) \int_0^(\infty) z^2|\Psi_(100)|^2 r^2 \sin\theta \,dr\, d\theta\, d\phi\]`

b. For the potential energy, in the state
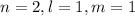`\(n=2, l=1, m=1\)`, the potential energy
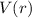`\(V(r)\)` for the hydrogen atom is given by:

`\[V(r) = -(e^2)/(4\pi\epsilon_0 r)\]`

where e is the elementary charge,
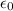`\(\epsilon_0\)` is the vacuum permittivity, and r is the distance from the nucleus.

The expectation value of the potential energy
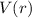`\(V(r)\)` for the electron in this state can be calculated similarly using the wave function of that state. It involves an integral like:

`\[ \langle V(r) \rangle = \int_0^(2\pi) \int_0^(\pi) \int_0^(\infty) V(r)|\Psi_(n,l,m)|^2 r^2 \sin\theta \,dr\, d\theta\, d\phi \]`

Substitute the respective wave function
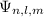`\(\Psi_(n,l,m)\)` for the state
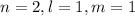`\(n=2, l=1, m=1\)` and evaluate the integral to find the expectation value of the potential energy in that state.