Question

A sample of 10 measurement of the diameter of a sphere gave a mean X = 4.38 centimeters (cm) and a standard deviation s = 0.06 cm. Find the (a) 95% and (b) 99% confidence limits for the actual diameter.

Answer 1

(a) 95% confidence limits

Upper limit = 4.4229 cm

Lower limit = 4.3371 cm

Confidence interval: (4.3371, 4.4229) (cm)

(b) 99% confidence limits

Upper limit = 4.4417 cm

Lower limit = 4.3183 cm

Confidence Interval: (4.3183, 4.4417) (cm)

Explanation:

Sample size = n = 10

X = 4.38 cm

s = 0.06 cm

Since sample size is 10, we use the t-table to find the limits.

For the 2-tailed 95% case, we get an alpha of 0.025

α = 0.025

Number of degrees of freedom = sample size - 1 = 10 - 1

Number of degrees of freedom = 9

Using the degrees of freedom and α value, we find the t-score,

we get (from a t-table),

We get t-score = t = 2.262

Now, to get the error, we have the formula,

`error = t*s/√(n)`

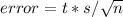
Putting values, we get,

`error = 2.262*0.06/√(10)\\ error = 0.0429`

Adding and subtracting from the mean to get the interval limits,

Upper limit = 4.38 + 0.0429 = 4.4229

Upper limit = 4.4229 cm

Lower limit = 4.38 - 0.0429 = 4.3371

Lower limit = 4.3371 cm

b) 99% confidence limits

For 99% we get an alpha value of,

α = (1-0.99)/2

α = 0.005

For which we get a t- value of,

t-score = 3.250

(all specific values are written on last part e.g degrees of freedom and so on)

Finding error,

`error = 3.250*0.06/√(10)\\ error = 0.0617`

Finding the upper and lower limits,

Upper limit = 4.38 + 0.0617 = 4.4417

Upper limit = 4.4417 cm

Lower limit = 4.38 - 0.0617 = 4.3183

Lower limit = 4.3183 cm

The confindence interval is (4.3183,4.4417)