Answer:
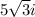
Explanation:
The square root of -75 is not a real number, because it is not possible to find a real number that when squared results in a negative number.
In mathematics, the square root of a number is defined as the number that, when multiplied by itself, equals the original number. For example, the square root of 4 is 2, because 2 x 2 = 4. Similarly, the square root of 9 is 3, because 3 x 3 = 9.
However, it is not possible to find a real number that, when squared, results in a negative number. This is because any real number multiplied by itself is always positive, regardless of whether the original number was positive or negative. For example, the square of -2 is 4, because (-2) × (-2) = 4, which is a positive number.
Double however, complex numbers are used to represent numbers that have a non-zero imaginary component, such as the square root of -1. Complex numbers are written in the form a + bi, where a and b are real numbers and i represents the imaginary unit.
Therefore, the square root of -75 can be written in simplified form as
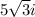 , where
, where
 is the imaginary unit. This represents a complex number with a real component of 0 and an imaginary component of
is the imaginary unit. This represents a complex number with a real component of 0 and an imaginary component of
 .
.