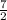Answer:
m = - 1 , m = 0 , m =
Explanation:
2m³ - 5m² - 7m = 0 ← factor out common factor m from each term
m(2m² - 5m - 7) = 0
factorise the quadratic 2m² - 5m - 7
consider the factors of the product of the coefficient of the m² term and the constant term which sum to give the coefficient of the m- term
product = 2 × - 7 = - 14 and sum = - 5
the factors are + 2 and - 7
use these factors to split the m- term
2m² + 2m - 7m - 7 ( factor the first/second and third/fourth terms )
2m(m + 1) - 7(m + 1) ← factor out (m + 1) from each term
(m + 1)(2m - 7)
then
2m³ - 5m² - 7m = 0
m(m + 1)(2m - 7) = 0 ← in factored form
equate each factor to zero and solve for m
m = 0
m + 1 = 0 ( subtract 1 from both sides )
m = - 1
2m - 7 = 0 ( add 7 to both sides )
2m = 7 ( divide both sides by 2 )
m =
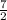
solutions are m = - 1 , m = 0 , m =