Question

Help please it's due tomorrow
​

Answer 1

SolutioN:-

`\{ \: \alpha \: , \: \beta , \: a, \: b \}`

`\sf \longrightarrow \: No. \: of \: \: subsets = {2}^(n)`

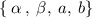
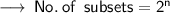
where, n denotes to number of elements in set .

Since, given set contains 4 elements .

Thus , 2⁴ {2 raise to power 4} .

`\sf \longrightarrow \: No. \: of \: \: subsets = {2}^(4)`

`\sf \longrightarrow \: No. \: of \: \: subsets = 2 * 2 * 2 * 2`

`\sf \longrightarrow \: No. \: of \: \: subsets = 4 * 4`

`\sf \longrightarrow \: No. \: of \: \: subsets = 16`

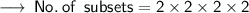
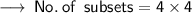
Therefore, Required subsets are 16.

They are , Namely;

`\sf \longrightarrow \: subsets \: = \phi \: \{ \alpha \} \{ \beta \} \{ a\} \{ b\} \: \{ \alpha \beta \} \{ \alpha a\} \{ \alpha b\} \{ \beta a\} \{ \beta b\} \: .....`

_____________________________

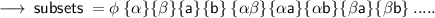
Additional Information:-

If n is the number of elements in the set then,

No. of subsets possible for this subset is 2^n that's the (2 raise to the power n).

Let's take another example, {1,2}

Here, n = 2

subsets =2^2 =4

Subsets = ϕ, {1}, {2},{1,2}

Note :- every set is a subset of itself i.e. {1,2} and ϕ is a subset of every set