Loan (a) has an annual effective yield (AEY) of 6.888%.
Loan (b) carries an AEY of 0.116745.
Loan (c) yields 0% in annual effective yield.
The weighted average AEY for the package of loans is 3.1335%.
Let's break down each loan and calculate the annual effective yield (AEY) for each one separately.
Loan (a)
- Principal (P) = $120,000
- Time (n) = 10 years
- Nominal discount rate (i) = 6.8% convertible monthly
Using the formula for the effective interest rate for monthly payments:
![\[ i_{\text{monthly}} = \frac{{(1 + i_{\text{annual}})^(1/m) - 1}}{1/m} \]](https://img.qammunity.org/2024/formulas/business/high-school/rh2dn48mqxv3uh3utf92phn5wt0xqpefrg.png)
Where
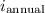 is the annual nominal rate,
is the annual nominal rate,
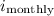 is the monthly nominal rate, and m is the number of compounding periods per year.
is the monthly nominal rate, and m is the number of compounding periods per year.
For Loan (a):
![\[ i_{\text{monthly}} = \frac{{(1 + 0.068)^(1/12) - 1}}{1/12} \]](https://img.qammunity.org/2024/formulas/business/high-school/5so3n55n5kq73r5vjh6lrknyv5dr4ts1xk.png)
Let's calculate
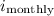 :
:
![\[ i_{\text{monthly}} = \frac{{(1.068)^(0.0833) - 1}}{0.0833} \approx 0.005521 \]](https://img.qammunity.org/2024/formulas/business/high-school/cwe9odafr6ojx1jmwt74oj9tubite8escy.png)
Now, we'll use the formula for the effective annual interest rate:
![\[ i_{\text{annual}} = (1 + i_{\text{monthly}})^(12) - 1 \]](https://img.qammunity.org/2024/formulas/business/high-school/lg09py2t2x0vop3d0q54mnhz11fgxj30uh.png)
Calculating
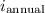 :
:
![\[ i_{\text{annual}} = (1 + 0.005521)^(12) - 1 \approx 0.06888 \]](https://img.qammunity.org/2024/formulas/business/high-school/yu2tb13zr323ehcng2ys678rgerw4hk6fw.png)
The annual effective yield (AEY) for Loan (a) is approximately 6.888%.
Loan (b)
For Loan (b), there are sinking fund payments. The interest rate for assessing the loan is 5.4% nominal convertible monthly, and the sinking fund earns 4% nominal interest convertible monthly.
Let's first calculate the sinking fund factor using the sinking fund formula:
![\[ \text{Sinking Fund Factor} = \frac{{i - j}}{{(1 + j)^n - 1}} \]](https://img.qammunity.org/2024/formulas/business/high-school/5k76j5y0zqxkvzheibhg5f8zs9ss0oz6z8.png)
Where:
- i = interest rate for assessing the loan = 5.4% = 0.054
- j = sinking fund interest rate = 4% = 0.04
- n = time = 10 years
![\[ \text{Sinking Fund Factor} = \frac{{0.054 - 0.04}}{{(1 + 0.04)^(10) - 1}} \]](https://img.qammunity.org/2024/formulas/business/high-school/xvtmet1lc7pgv2wl8ykhtqmsyilhrwh5pr.png)
Let's calculate the Sinking Fund Factor:
![\[ \text{Sinking Fund Factor} = \frac{{0.014}}{{(1.04)^(10) - 1}} \approx 0.116745 \]](https://img.qammunity.org/2024/formulas/business/high-school/zvsw6rrv41q09yelqsnl9hefmlc1e2vmvl.png)
The sinking fund factor was approximately 0.116745.
Loan (c)
For Loan (c), it's a single payment of $200,000 with an effective rate of discount of 8.2% throughout the ten years. The calculation for this is a direct application of the effective interest rate formula:
![\[ i_{\text{annual}} = \frac{{F - P}}{{P}} \]](https://img.qammunity.org/2024/formulas/business/high-school/qqwc43c0m2h7aofb8l36l4irvyha6qtmzk.png)
Where:
- F = future value = $200,000
- P = present value = $200,000
- n = time = 10 years
![\[ i_{\text{annual}} = \frac{{200,000 - 200,000}}{{200,000}} = 0 \]](https://img.qammunity.org/2024/formulas/business/high-school/1f1yzlpuijft60usukvwlfys8jfku28st1.png)
The effective annual yield for Loan (c) is 0%.
Package of Loans
Now, let's find the weighted average AEY for the package of loans:
![\[ \text{Weighted Average AEY} = (0.2857 * 6.888\%) + (0.2381 * 4.8931\%) + (0.4762 * 0\%) \]](https://img.qammunity.org/2024/formulas/business/high-school/ymm3lq5nozz44bshb2arq44zx2p34vu36x.png)
Calculating the weighted average AEY:
![\[ \text{Weighted Average AEY} = (0.2857 * 6.888\%) + (0.2381 * 4.8931\%) \]](https://img.qammunity.org/2024/formulas/business/high-school/3ehfwq3foddhgkrk9mw4h94an9fc6iik93.png)
![\[ \text{Weighted Average AEY} = 1.9673\% + 1.1662\% \]](https://img.qammunity.org/2024/formulas/business/high-school/z4gbzsny7jsgsd6kmklcovn7wr48t460dl.png)
![\[ \text{Weighted Average AEY} = 3.1335\% \]](https://img.qammunity.org/2024/formulas/business/high-school/7hzywv2w5sr6xvlukumlcsbuiyjw3ta0gp.png)
The weighted average annual effective yield (AEY) for the package of loans over the ten-year period is approximately 3.1335%.