Question

Calculate the molar solubility of XF \( 2,\left(\mathrm{Ksp}=5.3 \times 10^{-6}\right) \) in a \( 0.199 \mathrm{MX}\left(\mathrm{NO}_{3}\right. \) ) solution Report your answer with 4 decimal places

Answer 1

To calculate the molar solubility of XF₂ in a 0.199 M X(NO₃)₂ solution, we need to use the solubility product constant (Ksp) and the stoichiometry of the balanced equation.

The balanced equation for the dissolution of XF₂ is:

`\displaystyle\sf XF_(2)(s) \rightarrow X^(2+)(aq) + 2F^(-)(aq)`

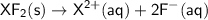
According to the equation, 1 mole of XF₂ produces 1 mole of X²⁺ ions and 2 moles of F⁻ ions.

Let's assume the molar solubility of XF₂ is represented by "x" (in mol/L).

The equilibrium expression for the solubility product (Ksp) is:

`\displaystyle\sf Ksp = [X^(2+)] * [F^(-)]^2`

Given that Ksp = 5.3 x 10⁻⁶ and the concentration of X(NO₃)₂ is 0.199 M, we can set up the following equation:

`\displaystyle\sf 5.3 * 10^(-6) = x * (2x)^2`

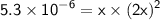
Solving for "x," we find:

`\displaystyle\sf x \approx \sqrt[3]{(5.3 * 10^(-6))/(4)}`

Calculating the result, we get:

`\displaystyle\sf x \approx 0.0197`

Therefore, the molar solubility of XF₂ in the 0.199 M X(NO₃)₂ solution is approximately 0.0197 mol/L.