Let's solve the problem step by step:
Let's assume the first even number as
 .
.
The next consecutive even number can be represented as
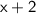 .
.
According to the given information, the sum of the squares of these two numbers is 52:

Expanding the equation:
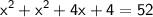
Combining like terms:
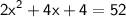
Subtracting 52 from both sides:
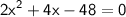
Dividing the equation by 2 to simplify:
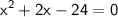
Factoring the quadratic equation:
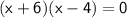
Setting each factor equal to zero and solving for
 :
:
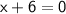 or
or
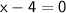
If
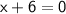 , then
, then
 . However, since we are looking for positive even numbers,
. However, since we are looking for positive even numbers,
 is not valid.
is not valid.
If
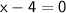 , then
, then
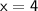 .
.
Therefore, the first even number is 4, and the next consecutive even number is
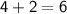 .
.
So the two numbers are 4 and 6.

♥️
