Question

A kite has a height of 36 inches and a width of 30 inches. Explain how to use the area formula for a triangle to find the area of the kite.

On Edge so if you know it please help! I NEED THE ANSWER A S A P

Answer 1

To find the area of the kite, we can use the area formula for a triangle since a kite can be divided into two congruent triangles. The formula for the area of a triangle is:

`\displaystyle\sf A=(1)/(2) * \text{base} * \text{height}`

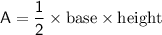
In the case of the kite, we can consider one of the diagonals as the base and the other diagonal as the height. Since the kite is symmetric, we can choose any diagonal as the base and the other diagonal as the height. Let's assume we choose the width of the kite (30 inches) as the base and the height of the kite (36 inches) as the height.

Using the area formula for a triangle, the area of one of the triangles formed by the diagonals of the kite is:

`\displaystyle\sf A_{\text{triangle}}=(1)/(2) * \text{base} * \text{height}`

`\displaystyle\sf A_{\text{triangle}}=(1)/(2) * 30 * 36`

`\displaystyle\sf A_{\text{triangle}}=540`

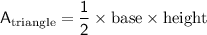
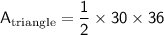
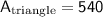
Since the kite is made up of two congruent triangles, we can multiply the area of one triangle by 2 to find the total area of the kite:

`\displaystyle\sf A_{\text{kite}}=2 * A_{\text{triangle}}`

`\displaystyle\sf A_{\text{kite}}=2 * 540`

`\displaystyle\sf A_{\text{kite}}=1080`

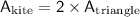
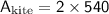
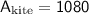
Therefore, the area of the kite is 1080 square inches, obtained by using the area formula for a triangle and multiplying it by 2 since the kite consists of two congruent triangles.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`