Certainly! I'd be happy to explain the question and help you understand the answer.
The given question is:
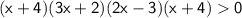 .
.
To solve this inequality, we need to determine the values of
 for which the expression
for which the expression
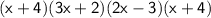 is greater than zero (
is greater than zero (
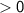 ).
).
To find the solution, we can use the concept of interval notation and zero-product property. Here's how we can proceed step by step:
1. Begin by finding the critical values of
 where the expression changes sign. These occur when any of the factors are equal to zero. From the given equation, we have:
where the expression changes sign. These occur when any of the factors are equal to zero. From the given equation, we have:

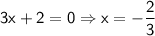
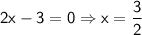
2. Now, we have four critical values:
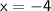 ,
,
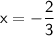 ,
,
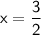 , and
, and
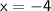 (since
(since
 yields
yields
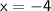 as well).
as well).
3. Plot these critical values on a number line:

4. Now, we need to test the expression
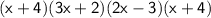 in the intervals created by these critical values. We will choose test points within each interval and determine if the expression is positive or negative.
in the intervals created by these critical values. We will choose test points within each interval and determine if the expression is positive or negative.
For example, let's take a test point
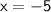 from the interval
from the interval
 :
:
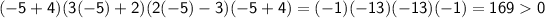
Since the expression
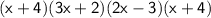 is positive in the interval
is positive in the interval
 , this interval is part of the solution.
, this interval is part of the solution.
By repeating this process for the remaining intervals, you'll find that the complete solution to the given inequality is:

In interval notation, the solution is:
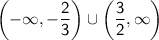

♥️
